
【题目】已知函数 ![]() 与
与 ![]() (其中
(其中 ![]() )在
)在 ![]() 上的单调性正好相反,回答下列问题:
上的单调性正好相反,回答下列问题:
(1)对于 ![]() ,
, ![]() ,不等式
,不等式 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围;
的取值范围;
(2)令 ![]() ,两正实数
,两正实数 ![]() 、
、 ![]() 满足
满足 ![]() ,求证:
,求证: ![]() .
.
【答案】
(1)因为 ![]() ,所以
,所以 ![]() ,
,
①当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为减函数;
上为减函数;
②当a>-1时, ![]() ,
,
令 ![]() ,得
,得 ![]() ,此时
,此时 ![]() 在
在 ![]() 上为增函数;
上为增函数;
令 ![]() ,得
,得 ![]() ,此时
,此时 ![]() 在
在 ![]() 上为减函数;
上为减函数;
又因为 ![]() ,则
,则 ![]() ,
,
①当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为增函数;
上为增函数;
②当a>0时, ![]() ,
,
令 ![]() ,得
,得 ![]() ,此时
,此时 ![]() 在
在 ![]() 上为增函数;
上为增函数;
令 ![]() ,得
,得 ![]() ,此时
,此时 ![]() 在
在 ![]() 上为增函数;
上为增函数;
于是若要 ![]() 与
与 ![]() 在
在 ![]() 上的单调性正好相反,
上的单调性正好相反,
则必须 ![]() ,解得
,解得 ![]() ,
,
∴ ![]() ,
,
所以,函数 ![]() 在
在 ![]() 上单调递减,
上单调递减, ![]() 上单调递增.
上单调递增.
∴在区间 ![]() 上:
上:
对于函数 ![]() 有
有 ![]()
又 ![]() ,
,
∴ ![]() .
.
对于函数 ![]() 有
有 ![]()
又 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
综上,所求t的范围为 ![]()
(2)易得 ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]()
∴ ![]()
∴ ![]()
令,设 ![]() ,则
,则 ![]() ,
,
可知 ![]() 在
在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减,
上单调递减,
∴ ![]() ,
,
∴ ![]()
【解析】本题主要考查不等式恒成立问题的求解,导数在研究函数中的应用,意在考查逻辑思维能力和分析问题、解决问题的综合能力.
【考点精析】认真审题,首先需要了解基本不等式(基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ).
).


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax+2lnx(其中a是实数).
(1)求f(x)的单调区间;
(2)若设2(e+ ![]() )<a<
)<a< ![]() ,且f(x)有两个极值点x1 , x2(x1<x2),求f(x1)﹣f(x2)取值范围.(其中e为自然对数的底数).
,且f(x)有两个极值点x1 , x2(x1<x2),求f(x1)﹣f(x2)取值范围.(其中e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 分别是椭圆
分别是椭圆 ![]() 的左、右焦点,离心率为
的左、右焦点,离心率为 ![]() ,
, ![]() ,
, ![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点, ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)过 ![]() (0,2)作直线
(0,2)作直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,求三角形
两点,求三角形 ![]() 面积的最大值(
面积的最大值( ![]() 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品每吨的价格为x(1<x<14)万元时,该商品的月供给量为y1吨,y1=ax+ ![]() a2﹣a(a>0):月需求量为y2吨,y2=﹣
a2﹣a(a>0):月需求量为y2吨,y2=﹣ ![]() x2﹣
x2﹣ ![]() x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
(1)已知a= ![]() ,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f'(x)是函数f(x)的导数,f'(x)是函数f'(x)的导数,若方程f'(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数f(x)的拐点.某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,
设函数g(x)=x3﹣3x2+4x+2,利用上述探究结果
计算: ![]() =
=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的组合体中,三棱柱ABC﹣A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点. 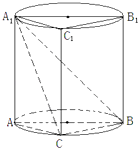
(Ⅰ)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线A1C与AB1的所成角的大小;
(Ⅱ)当点C是弧AB的中点时,求四棱锥A1﹣BCC1B1与圆柱的体积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com