
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(Ⅰ)证明:取PB的中点F,连接AF,EF. ∵EF是△PBC的中位线,∴EF∥BC,且EF= ![]() .
.
又AD=BC,且AD= ![]() ,∴AD∥EF且AD=EF,
,∴AD∥EF且AD=EF,
则四边形ADEF是平行四边形.
∴DE∥AF,又DE面ABP,AF面ABP,
∴ED∥面PAB;
(Ⅱ)解:法一、取BC的中点M,连接AM,则AD∥MC且AD=MC,
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上.
∴AB⊥AC,可得 ![]() .
.
过D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,则DG⊥PC.
过G作GH⊥PC于H,则PC⊥面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中, ![]() ,连接AE,
,连接AE, ![]() .
.
在Rt△GDH中, ![]() ,
,
∴ ![]() ,
,
即二面角A﹣PC﹣D的余弦值 ![]() .
.
法二、取BC的中点M,连接AM,则AD∥MC,且AD=MC.
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
如图以A为原点, ![]() 方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
可得 ![]() ,
, 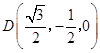 .
.
设P(x,0,z),(z>0),依题意有 ![]() ,
, ![]() ,
,
解得 ![]() .
.
则  ,
,  ,
,  .
.
设面PDC的一个法向量为 ![]() ,
,
由 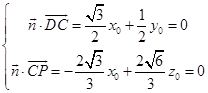 ,取x0=1,得
,取x0=1,得  .
.![]() 为面PAC的一个法向量,且
为面PAC的一个法向量,且 ![]() ,
,
设二面角A﹣PC﹣D的大小为θ,
则有  ,即二面角A﹣PCD的余弦值
,即二面角A﹣PCD的余弦值 ![]() .
.

【解析】(Ⅰ)取PB的中点F,连接AF,EF,由三角形的中位线定理可得四边形ADEF是平行四边形.得到DE∥AF,再由线面平行的判定可得ED∥面PAB;(Ⅱ)法一、取BC的中点M,连接AM,由题意证得A在以BC为直径的圆上,可得AB⊥AC,找出二面角A﹣PC﹣D的平面角.求解三角形可得二面角A﹣PC﹣D的余弦值. 法二、由题意证得AB⊥AC.又面PAC⊥平面ABCD,可得AB⊥面PAC.以A为原点, ![]() 方向分别为x轴正方向,y轴正方向建立空间直角坐标系.求出P的坐标,再求出平面PDC的一个法向量,由图可得
方向分别为x轴正方向,y轴正方向建立空间直角坐标系.求出P的坐标,再求出平面PDC的一个法向量,由图可得 ![]() 为面PAC的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PC﹣D的余弦值.
为面PAC的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PC﹣D的余弦值.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)当二面角A﹣PB﹣E的余弦值为多少时,直线PC与平面PAB所成的角为45°?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣2ax,a∈R.
(1)若函数y=f(x)存在与直线2x﹣y=0平行的切线,求实数a的取值范围;
(2)设g(x)=f(x)+ ![]() ,若g(x)有极大值点x1 , 求证:
,若g(x)有极大值点x1 , 求证: ![]() >a.
>a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( ) 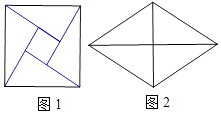
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增一十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?( )
A.8日
B.9日
C.12日
D.16日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ﹣1),
﹣1), ![]() =(
=( ![]() sin
sin ![]() ,cos2
,cos2 ![]() ),函数f(x)=
),函数f(x)= ![]() +1.
+1.
(1)若x∈[ ![]() ,π],求f(x)的最小值及对应的x的值;
,π],求f(x)的最小值及对应的x的值;
(2)若x∈[0, ![]() ],f(x)=
],f(x)= ![]() ,求sinx的值.
,求sinx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 与
与 ![]() (其中
(其中 ![]() )在
)在 ![]() 上的单调性正好相反,回答下列问题:
上的单调性正好相反,回答下列问题:
(1)对于 ![]() ,
, ![]() ,不等式
,不等式 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围;
的取值范围;
(2)令 ![]() ,两正实数
,两正实数 ![]() 、
、 ![]() 满足
满足 ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com