
【题目】已知抛物线y2=2px(p>0)的焦点为F,直线y=x﹣8与此抛物线交于A、B两点,与x轴交于点C,O为坐标原点,若 ![]() =3
=3 ![]() .
.
(1)求此抛物线的方程;
(2)求证:OA⊥OB.
【答案】
(1)
解:抛物线y2=2px(p>0),焦点F( ![]() ,0),
,0),
直线y=x﹣8与x轴交于点C,即C(8,0),
∵ ![]() =3
=3 ![]() .即3
.即3 ![]() =8﹣
=8﹣ ![]() ,解得:p=4
,解得:p=4
∴抛物线的方程为y2=8x
(2)
证明:由 ![]() ,得y2=8(y+8),即y2﹣8y﹣64=0,
,得y2=8(y+8),即y2﹣8y﹣64=0,
设A(x1,y1),B(x2,y2),
∴y1y2=﹣64,
又 ![]() ,
,
∴ ![]()
![]() =x1x2+y1y2=64﹣64=0,
=x1x2+y1y2=64﹣64=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴OA⊥OB
【解析】(1)由抛物线y2=2px(p>0),焦点F( ![]() ,0),C(8,0),由
,0),C(8,0),由 ![]() =3
=3 ![]() ,可得3×
,可得3× ![]() =8﹣
=8﹣ ![]() ,即可求得p的值,求得抛物线的方程;(2)将直线方程代入抛物线方程,由韦达定理定理可知:y1y2=﹣64,代入求得x1x2 , 由
,即可求得p的值,求得抛物线的方程;(2)将直线方程代入抛物线方程,由韦达定理定理可知:y1y2=﹣64,代入求得x1x2 , 由 ![]()
![]() =x1x2+y1y2=0,可知
=x1x2+y1y2=0,可知 ![]() ⊥
⊥ ![]() ,因此OA⊥OB.
,因此OA⊥OB.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意m∈R,直线mx﹣y+1=0与圆x2+y2=r2(r>0)交于不同的两点A、B,且存在m使| ![]() +
+ ![]() |≥|
|≥| ![]() |(O是坐标原点)成立,那么r的取值范围是( )
|(O是坐标原点)成立,那么r的取值范围是( )
A.0<r≤ ![]()
B.1<r< ![]()
C.1<r≤ ![]()
D.r> ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() =1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线的两条渐近线交于B、C两点,过B、C分别作AC、AB的垂线,两垂线交于点D.若D到直线BC的距离小于2(a+
=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线的两条渐近线交于B、C两点,过B、C分别作AC、AB的垂线,两垂线交于点D.若D到直线BC的距离小于2(a+ ![]() ),则该双曲线的离心率的取值范围是( )
),则该双曲线的离心率的取值范围是( )
A.(1,2)
B.( ![]() ,2)
,2)
C.(1, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上(异于端点),设a,b,c,p均为非零实数,直线BP,CP分别交AC,AB于点E,F,一同学已正确算的OE的方程:( ![]() ﹣
﹣ ![]() )x+(
)x+( ![]() ﹣
﹣ ![]() )y=0,请你求OF的方程:()x+(
)y=0,请你求OF的方程:()x+( ![]() ﹣
﹣ ![]() )y=0.
)y=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
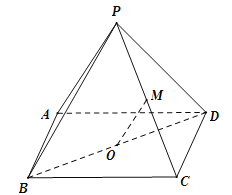
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的方程ax2+2x+1=0至少有一个负根,q:a≤1,则¬p是¬q的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,连结
的中点,连结![]() .求证:
.求证:

(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间. 
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com