
【题目】已知函数![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个不同零点
有两个不同零点![]() ,
,![]() ,证明:
,证明:![]() 且
且![]() .
.
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)求导后,令![]() 得
得![]() 或
或![]() ,按照
,按照![]() 与
与![]() 的大小分三种情况讨论即可得到答案;
的大小分三种情况讨论即可得到答案;
(2)根据(1)知![]() 时,函数的极小值大于0,因此函数
时,函数的极小值大于0,因此函数![]() 不可能有2个零点,故
不可能有2个零点,故![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以极小值
单调递增,所以极小值![]() ,可得
,可得![]() ,再构造函数
,再构造函数![]() ,利用导数得到
,利用导数得到![]() 在
在![]() 上递增,从而可得
上递增,从而可得![]() 时,
时,![]() ,设
,设![]() ,则
,则![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 。
。
(1)![]() .
.
因为![]() ,由
,由![]() 得,
得,![]() 或
或![]() .
.
i)![]() 即
即![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
ii)![]() 即
即![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
iii)![]() 即
即![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)由(1)知,![]() 时,
时,![]() 的极小值为
的极小值为![]() ,
,
![]() 时,
时,![]() 的极小值为
的极小值为![]() ,
,
![]() 时,
时,![]() 在
在![]() 单调,
单调,
故![]() 时,
时,![]() 至多有一个零点.
至多有一个零点.
当![]() 时,易知
时,易知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
要使![]() 有两个零点,则
有两个零点,则![]() ,即
,即![]() ,得
,得![]() .
.
令![]() ,(
,(![]() ),则
),则![]()
![]()
![]()
![]() ,所以
,所以![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,![]() .
.
不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]() .
.
由![]() 在
在![]() 单调递减得,
单调递减得,![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】学校准备将![]() 名同学全部分配到运动会的田径、拔河和球类
名同学全部分配到运动会的田径、拔河和球类![]() 个不同项目比赛做志愿者,每个项目至少
个不同项目比赛做志愿者,每个项目至少![]() 名,则不同的分配方案有________种(用数字作答).
名,则不同的分配方案有________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
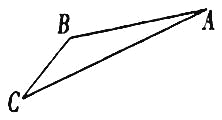
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题
①命题“若![]() ,则
,则![]() ”的逆命题是真命题;
”的逆命题是真命题;
②若![]() ,
,![]() ,则
,则![]() 在
在![]() 上的投影是
上的投影是![]() ;
;
③在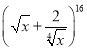 的二项展开式中,有理项共有4项;
的二项展开式中,有理项共有4项;
④已知一组正数![]() ,
,![]() ,
,![]() ,
,![]() 的方差为
的方差为![]() ,则数据
,则数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数为4;
的平均数为4;
⑤复数![]() 的共轭复数是
的共轭复数是![]() ,则
,则![]() .
.
其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() .
.
(1)若![]() ,试判断
,试判断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对(2)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立,若存在,求出数列
都成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ;
;
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() ,且
,且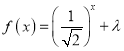 在闭区间
在闭区间![]() 上有实数解,求实数
上有实数解,求实数![]() 的范围;
的范围;
(3)如果函数![]() 的图象过点
的图象过点![]() ,且不等式
,且不等式![]() 对任意
对任意![]() 均成立,求实数
均成立,求实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直二面角α﹣l﹣β中,A∈α,B∈β,A,B都不在l上,AB与α所成角为x,AB与β所成角为y,AB与l所成角为z,则cos2x+cos2y+sin2z的值为( )
A.![]() B.2C.3D.
B.2C.3D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品每吨的价格为![]() 万元时,该商品的月供给量为
万元时,该商品的月供给量为![]() 吨,
吨,![]() ;月需求量为
;月需求量为![]() 吨,
吨,![]() ,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
(1)已知![]() ,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com