Question

【题目】在极坐标系中，曲线的方程为，以极点为原点，极轴所在直线为轴建立直角坐标，直线的参数方程为（为参数），与交于，两点．

（1）写出曲线的直角坐标方程和直线的普通方程；

（2）设点；若、、成等比数列，求的值

Answer 1

【答案】(1) 曲线的直角坐标方程为，直线的普通方程为 ； (2)

【解析】

(1)由极坐标与直角坐标的互化公式和参数方程与普通方程的互化，即可求解曲线的直角坐标方程和直线的普通方程；

(2)把的参数方程代入抛物线方程中，利用韦达定理得，，可得到，根据因为，，成等比数列，列出方程，即可求解．

(1)由题意，曲线的极坐标方程可化为，

又由，可得曲线的直角坐标方程为，

由直线的参数方程为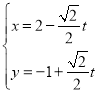（为参数），消去参数，得，

即直线的普通方程为；

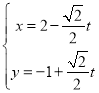(2)把的参数方程代入抛物线方程中，得，

由，设方程的两根分别为，，

则，，可得，．

所以，，．

因为，，成等比数列，所以，即，

则，解得解得或（舍），

所以实数.