
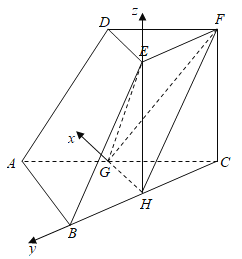
【题目】如图,在三棱台![]() 中,
中,![]() ,G,H分别为
,G,H分别为![]() ,
,![]() 上的点,平面
上的点,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
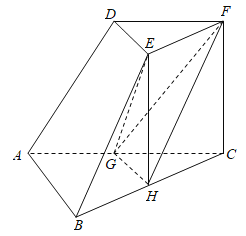
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明![]() ,
,![]() 得到
得到![]() 平面
平面![]() ,得到答案.
,得到答案.
(2)分别以![]() ,
,![]() ,
,![]() 所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系
所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系![]() ,计算平面
,计算平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为
![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
因为![]() ,所以
,所以![]() ,H为
,H为![]() 的中点.
的中点.
同理G为![]() 的中点,所以
的中点,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
又![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
分别以![]() ,
,![]() ,
,![]() 所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系
所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,因为
,因为![]() ,
,![]()
则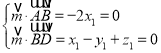 ,取
,取![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,因为
,因为![]() ,
,![]()
则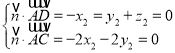 ,取
,取![]() ,得
,得![]() .
.
所以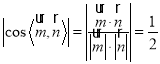 ,则二面角
,则二面角![]() 的大小为
的大小为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在这智能手机爆发的时代,大部分高中生都有手机,在手机面前,有些学生无法抵御手机尤其是手机游戏和短视频的诱惑,从而导致无法专心完成学习任务,成绩下滑;但是对于自制力强,能有效管理自己的学生,手机不仅不会对他们的学习造成负面影响,还能成为他们学习的有力助手,我校某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,部分统计数据如表:
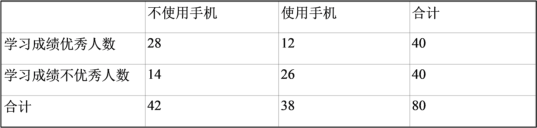
参考数据: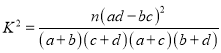 ,其中
,其中![]() .
.
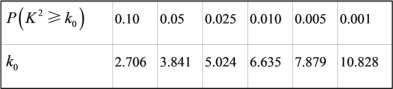
(1)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用手机对学习有影响?
(2)研究小组将该样本中不使用手机且成绩优秀的同学记为![]() 组,使用手机且成绩优秀的同学记为
组,使用手机且成绩优秀的同学记为![]() 组,计划从
组,计划从![]() 组推选的4人和
组推选的4人和![]() 组推选的2人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自
组推选的2人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自![]() 组、另一人来自
组、另一人来自![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 极点,以
极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
⑴ 求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
⑵ 试判断曲线![]() 与
与![]() 是否存在两个交点,若存在求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
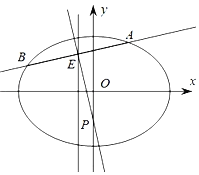
(1)求椭圆C的方程;
(2)直线l交椭圆C于不同的两点A、B,且![]() 中点E在直线
中点E在直线![]() 上,线段
上,线段![]() 的垂直平分线交y轴于点
的垂直平分线交y轴于点![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是生命之源,为了引导市民科学用水,我国加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变,“建机制”是制定合理的阶梯用水价格某城市采用简单随机抽样的方法从郊区和城区分别抽取5户和20户居民的年人均用水量(单位:吨)进行调研,抽取数据的茎叶图如下:
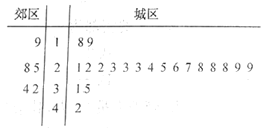
(1)若在郊区的这5户居民中随机抽取2户,求“被抽取的2户年人均用水量的和超过60吨”的概率;
(2)若该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,只保证这一梯次的居民用户用水价格不变,试根据样本估计总体的思想分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com