
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)若不等式![]() 对于任意
对于任意![]() 成立,求正实数
成立,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)![]() ,对a分类讨论以确定函数
,对a分类讨论以确定函数![]() 的单调增区间;(2)不等式
的单调增区间;(2)不等式![]() 对任意
对任意![]() 成立等价于对任意
成立等价于对任意![]() ,有
,有![]() 成立.设
成立.设![]() ,
,![]() ,则只要
,则只要![]() 即可.
即可.
(1)由题意得,函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
若![]() ,则当
,则当![]() 或
或![]() 时,
时,![]() ,此时
,此时![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.若
单调递减.若![]() ,则当
,则当![]() 时,
时,![]() ,此时
,此时![]() 单调递减;当
单调递减;当![]() 时,即
时,即![]() ,此时
,此时![]() 单调递增.
单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增.
上单调递增.
(2)不等式![]() 对任意
对任意![]() 成立等价于对任意
成立等价于对任意![]() ,有
,有![]() 成立.
成立.
设![]() ,
,![]() ,则只要
,则只要![]() 即可.
即可.
![]() .
.
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
所以函数![]() 在
在![]() 是哪个单调递减,在
是哪个单调递减,在![]() 上单调递增.
上单调递增.
所以![]() 的最大值为
的最大值为![]() 与
与![]() 中的较大者.
中的较大者.
设![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() .
.
从而![]() .所以
.所以![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() 的解为
的解为![]() .
.
因为![]() ,所以正实数
,所以正实数![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,有下列结论:
中,有下列结论:
①![]() 平面
平面![]() ;
;
②异面直线AD与![]() 所成的角为
所成的角为![]() ;
;
③三棱柱![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的四倍;
的体积的四倍;
④在四面体![]() 中,分别连接三组对棱的中点的线段互相垂直平分.
中,分别连接三组对棱的中点的线段互相垂直平分.
其中正确的是________(填出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
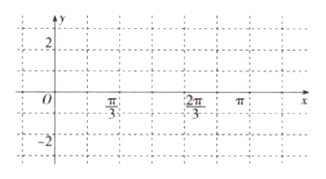
(1)请将上表数据补充完整,并写出函数![]() 的解析式(直接写出结果即可);
的解析式(直接写出结果即可);
(2)根据表格中的数据作出![]() 在一个周期内的图像;
在一个周期内的图像;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为了解该校学生对2017年全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类.已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)根据题意建立![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人进行回访,求这2人全是男生的概率.
参考公式和数据:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离A为
方向,距离A为![]() 海里的B处有一艘走私船,在A处北偏西
海里的B处有一艘走私船,在A处北偏西![]() 方向距离
方向距离![]() 为
为![]() 海里的
海里的![]() 处有我方一艘辑私艇奉命以
处有我方一艘辑私艇奉命以![]() 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以![]() 海里/小时的速度从
海里/小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com