
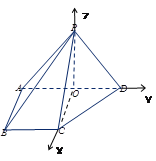
【题目】 如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.

(1) 求直线PB与平面POC所成角的余弦值;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】 (1) ![]() .(2)存在,
.(2)存在,![]() .
.
【解析】试题分析:由PA=PD, O为AD中点,侧面PAD⊥底面ABCD,可得PO⊥平面ABCD.又在直角梯形ABCD中,易得![]() ,所以可以O为坐标原点,OC为x轴,OD为y轴, OP为z轴建立空间直角坐标系,然后利用空间向量求解.
,所以可以O为坐标原点,OC为x轴,OD为y轴, OP为z轴建立空间直角坐标系,然后利用空间向量求解.
试题解析:(1)在![]() 中,
中,![]() ,
,![]() 为AD的中点,所以
为AD的中点,所以![]() ,
,
侧面PAD![]() 底面ABCD,PO
底面ABCD,PO![]() 面ABCD.又在直角梯形ABCD中,连接
面ABCD.又在直角梯形ABCD中,连接![]() ,则
,则![]() ,以O为坐标原点,直线OC为X轴,直线OD为Y轴,直线
,以O为坐标原点,直线OC为X轴,直线OD为Y轴,直线![]() 为Z轴建立空间直角坐标系.
为Z轴建立空间直角坐标系.![]() ,
,![]() ,
,![]() ,
, 
所以,直线PB与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(2) 假设存在,则设![]() =λ
=λ![]() (0<λ<1)
(0<λ<1)
因为![]() =(0,1,﹣1),所以Q(0,λ,1﹣λ).
=(0,1,﹣1),所以Q(0,λ,1﹣λ).
设平面CAQ的法向量为![]() =(a,b,c),则
=(a,b,c),则![]() ,
,
所以取![]() =(1﹣λ,λ﹣1,λ+1),
=(1﹣λ,λ﹣1,λ+1),
平面CAD的法向量![]() =(0,0,1),
=(0,0,1),
因为二面角Q﹣AC﹣D的余弦值为![]() ,
,
所以![]() =
=![]() ,
,
所以3λ2﹣10λ+3=0.
所以λ=![]() 或λ=3(舍去),
或λ=3(舍去),
所以![]() =
=![]() .
.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知两圆![]() ,
, ![]() 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且![]() .
.
(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:

(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,其中
,其中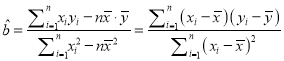 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,且其
,且其
三个顶点均在抛物线![]() 上.
上.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,与直线
,与直线![]()
相交于点![]() .证明以
.证明以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
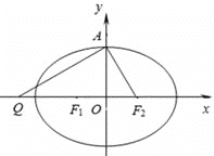
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为A,过点A与
,上顶点为A,过点A与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,若过
,若过![]() ,
, ![]() ,
, ![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切.过定点
相切.过定点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() ,
, ![]() 之间).
之间).
(Ⅰ)求椭圆![]() 的方程;(Ⅱ)若实数
的方程;(Ⅱ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=aln x+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数f(x)的解析式及单调区间;
(2)若函数g(x)=f(x)+m-ln 4在![]() 上恰有两个零点,求实数m的取值范围.
上恰有两个零点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com