
【题目】如图, ![]() 为正方形,
为正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
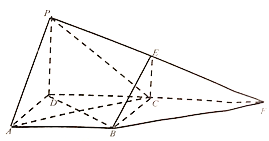
(1)若![]() 和
和![]() 延长交于点
延长交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 边上的动点,求直线
边上的动点,求直线![]() 与平面
与平面![]() 所成角正弦值的最小值.
所成角正弦值的最小值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据三角形中位线性质得![]() 为
为![]() 中点,再根据
中点,再根据![]() 为平行四边形得
为平行四边形得![]() ,最后根据线面平行判定定理得结论,(2)利用空间向量求线面角,关键求出平面法向量:先建立空间直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出直线方向向量与平面法向量夹角的余弦值,最后根据线面角与两向量夹角之间关系求线面角正弦值,再根据自变量取值范围求最小值.
,最后根据线面平行判定定理得结论,(2)利用空间向量求线面角,关键求出平面法向量:先建立空间直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出直线方向向量与平面法向量夹角的余弦值,最后根据线面角与两向量夹角之间关系求线面角正弦值,再根据自变量取值范围求最小值.
试题解析:(1)证明:在梯形PDCE中,PD=2EC, ![]() 为
为![]() 中点,
中点, ![]() ,且AB//CF,
,且AB//CF, ![]() 为平行四边形,
为平行四边形, ![]() 面
面![]() ,
, ![]() 面
面![]() ,
, ![]() BF∥平面PAC.
BF∥平面PAC.
(2)方法一:令点![]() 在面PBD上的射影为
在面PBD上的射影为![]() ,
, ![]() 直线
直线![]() 与平面PDB所成角.
与平面PDB所成角.
![]() EC∥PD,所以EC平行于平面PBD,因为ABCD为正方形,所以
EC∥PD,所以EC平行于平面PBD,因为ABCD为正方形,所以![]() ,又因为PD⊥平面ABCD,所以PD⊥AC,所以AC⊥平面PBD,所以点C到面PBD的距离为
,又因为PD⊥平面ABCD,所以PD⊥AC,所以AC⊥平面PBD,所以点C到面PBD的距离为![]() ,因为EC平行于平面PBD,所以点
,因为EC平行于平面PBD,所以点![]() 到PBD的距离
到PBD的距离![]() ,
,
令![]() ,所以
,所以![]() ,所以
,所以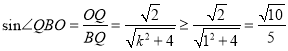 .
.
方法二:建立如图所示的空间直角坐标系O-xyz,可知平面PDB的一个法向量为![]() ,
, ![]() ,
, ![]() ,
,
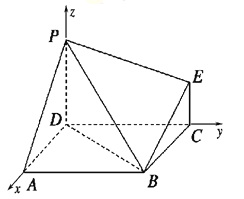
![]() ,令直线
,令直线![]() 与平面PDB所成角为
与平面PDB所成角为![]() ,
,
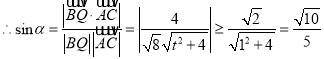 .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x≠1)
(x≠1)
(1)证明f(x)在(1,+∞)上是减函数;
(2)令g(x)=lnf(x),判断g(x)=lnf(x)的奇偶性并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
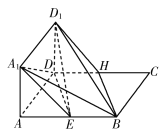
【题目】
如图所示,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() .
.
(1)若点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是( )
①P∈a,P∈αaα
②a∩b=P,bβaβ
③a∥b,aα,P∈b,P∈αbα
④α∩β=b,P∈α,P∈βP∈b.
A.①②
B.②③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足:
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)﹣1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)﹣1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2﹣2a﹣7)+ ![]() >0的解集为{a|﹣2<a<4},求f(5)的值.
>0的解集为{a|﹣2<a<4},求f(5)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知(a4﹣1)3+2016(a4﹣1)=1,(a2013﹣1)3+2016(a2013﹣1)=﹣1,则下列结论正确的是( )
A.S2016=﹣2016,a2013>a4
B.S2016=2016,a2013>a4
C.S2016=﹣2016,a2013<a4
D.S2016=2016,a2013<a4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
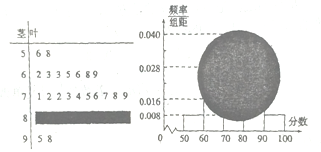
(1)求全班人数及分数在![]() 之间的频数;
之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中![]() 间的矩形的高;
间的矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com