
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:当![]() 时,
时,![]() .
.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 单调递增;当
单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减(2)证明见解析;
单调递减(2)证明见解析;
【解析】
(1)根据![]() ,求导得到
,求导得到![]() ,结合函数的定义域,分
,结合函数的定义域,分![]() 和
和![]() 两种情况讨论求解.
两种情况讨论求解.
(2)当![]() 时,
时,![]() ,将证明
,将证明![]() ,转化为证明
,转化为证明![]() 成立,令
成立,令![]() ,用导数法结合零点存在定理证明
,用导数法结合零点存在定理证明![]() 即可.
即可.
解法一:(1)因为![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
综上所述:当![]() 时,函数
时,函数![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)当![]() 时,
时,![]() ,
,
欲证![]() ,只需证
,只需证![]() ,即证明
,即证明![]() ,
,
令![]() ,
,
所以![]() ,
,
令![]() ,已知函数
,已知函数![]() 在
在![]() 单调递增.
单调递增.
又![]() ,
,![]() ,所以存在唯一
,所以存在唯一![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
所以函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以不等式![]() 成立,即当
成立,即当![]() 时,
时,![]() .
.
解法二:(1)同解法一
(2)当![]() 时,
时,![]() ,由(1)知:
,由(1)知:
![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,
,
即证![]() ,即只需证
,即只需证![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() 得
得![]() ;令
;令![]() 得
得![]() ,
,
所以函数![]() 在
在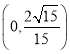 为减函数,在
为减函数,在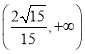 为增函数,
为增函数,
所以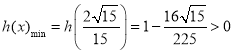 ,所以不等式
,所以不等式![]() 成立,
成立,
即当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,E是棱AB的中点,动点F是侧面ACC1A1(包括边界)上一点,若EF//平面BCC1B1,则动点F的轨迹是( )
A.线段B.圆弧
C.椭圆的一部分D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周髀算经》中,把圆及其内接正方形称为圆方图,把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑,它的正面图如图所示.以该木塔底层的边![]() 作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点
作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点![]() 正好位于塔身和塔顶的分界.经测量发现,木塔底层的边
正好位于塔身和塔顶的分界.经测量发现,木塔底层的边![]() 不少于
不少于![]() 米,塔顶
米,塔顶![]() 到点
到点![]() 的距离不超过
的距离不超过![]() 米,则该木塔的高度可能是(参考数据:
米,则该木塔的高度可能是(参考数据:![]() )( )
)( )

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
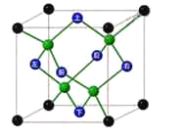
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的对称中心为原点
的对称中心为原点![]() ,焦点在
,焦点在![]() 轴上,焦距为
轴上,焦距为![]() ,点
,点![]() 在该椭圆上.
在该椭圆上.
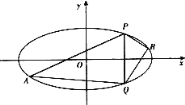
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 点位于第一象限,
点位于第一象限,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当点
两侧的动点.当点![]() 运动时,满足
运动时,满足![]() ,问直线
,问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,我国城市基础设施发生了巨大的变化,各种交通工具大大方便了人们的出行需求.某城市的A先生实行的是早九晚五的工作时间,上班通常乘坐公交或地铁加步行.已知从家到最近的公交站或地铁站都需步行5分钟,乘坐公交到离单位最近的公交站所需时间Z1(单位:分钟)服从正态分布N(33,42),下车后步行再到单位需要12分钟;乘坐地铁到离单位最近的地铁站所需时间Z2(单位:分钟)服从正态分布N(44,22),从地铁站步行到单位需要5分钟.现有下列说法:①若8:00出门,则乘坐公交一定不会迟到;②若8:02出门,则乘坐公交和地铁上班迟到的可能性相同;③若8:06出门,则乘坐公交比地铁上班迟到的可能性大;④若8:12出门,则乘坐地铁比公交上班迟到的可能性大.则以上说法中正确的序号是_____.
参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z≤μ+2σ)=0.9544,P(μ﹣3σ<Z≤μ+3σ)=0.9974
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com