
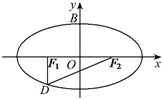
【题目】如图,设椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,点
,点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在![]() 轴上的圆,使圆在
轴上的圆,使圆在![]() 轴的上方与椭圆
轴的上方与椭圆
有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由题设知![]() 其中
其中![]()
由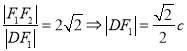 ,结合条件
,结合条件![]() 的面积为
的面积为![]() ,可求
,可求![]() 的值,再利用椭圆的定义和勾股定理即可求得
的值,再利用椭圆的定义和勾股定理即可求得![]() 的值,从而确定椭圆的标准方程;
的值,从而确定椭圆的标准方程;
(2)假设存在圆心在![]() 轴上的圆,使圆在
轴上的圆,使圆在![]() 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点;设圆心在
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点;设圆心在![]() 轴上的圆与椭圆在
轴上的圆与椭圆在![]() 轴的上方有两个交点为
轴的上方有两个交点为![]() 由圆的对称性可知
由圆的对称性可知![]() ,利用
,利用![]() 在圆上及
在圆上及![]() 确定交点的坐标,进而得到圆的方程.
确定交点的坐标,进而得到圆的方程.
解:(1)设![]() ,其中
,其中![]() ,
,
由![]() 得
得![]()
从而![]() 故
故![]() .
.
从而![]() ,由
,由![]() 得
得![]() ,因此
,因此![]() .
.
所以![]() ,故
,故![]()
因此,所求椭圆的标准方程为: ![]()
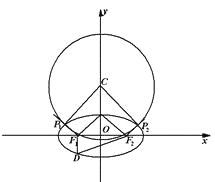
(2)如图,设圆心在![]() 轴上的圆
轴上的圆![]() 与椭圆
与椭圆![]() 相交,
相交, ![]() 是两个交点,
是两个交点, ![]() ,
, ![]() ,
,![]() 是圆
是圆![]() 的切线,且
的切线,且![]()
![]()
![]() 由圆和椭圆的对称性,易知
由圆和椭圆的对称性,易知![]()
![]() ,
,
由(1)知![]() ,所以
,所以![]() ,再由
,再由![]()
![]()
![]() 得
得![]() ,由椭圆方程得
,由椭圆方程得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时, ![]() 重合,此时题设要求的圆不存在.
重合,此时题设要求的圆不存在.
当![]() 时,过
时,过![]() 分别与
分别与![]() ,
,![]() 垂直的直线的交点即为圆心
垂直的直线的交点即为圆心![]() ,设
,设![]()
由![]() 得
得![]() 而
而![]() 故
故![]()
圆![]() 的半径
的半径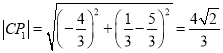
综上,存在满足条件的圆,其方程为: ![]()


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() ),g(x)=mcos(2x﹣
),g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若对任意x1∈[0,
)﹣2m+3(m>0),若对任意x1∈[0, ![]() ],存在x2∈[0,
],存在x2∈[0, ![]() ],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的袋子中装有![]() 个形状相同的小球,分别标有不同的数字
个形状相同的小球,分别标有不同的数字![]() ,现从袋中随机摸出
,现从袋中随机摸出![]() 个球,并计算摸出的这
个球,并计算摸出的这![]() 个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验.记
个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验.记![]() 事件为“数字之和为
事件为“数字之和为![]() ”.试验数据如下表:
”.试验数据如下表:

(1)如果试验继续下去,根据上表数据,出现“数字之和为![]() ”的频率将稳定在它的概率附近.试估计“出现数字之和为
”的频率将稳定在它的概率附近.试估计“出现数字之和为![]() ”的概率,并求
”的概率,并求![]() 的值;
的值;
(2)在(1)的条件下,设定一种游戏规则:每次摸![]() 球,若数字和为
球,若数字和为![]() ,则可获得奖金
,则可获得奖金![]() 元,否则需交
元,否则需交![]() 元.某人摸球
元.某人摸球![]() 次,设其获利金额为随机变量
次,设其获利金额为随机变量![]() 元,求
元,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线y=1﹣x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.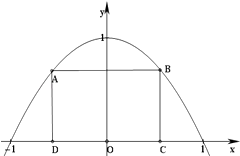
(1)求等待开垦土地的面积;
(2)如何确定点C的位置,才能使得整块土地总价值最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com