
【题目】已知![]() .
.
(1)当![]() 时,
时,![]() 的值域是
的值域是![]() ,试求实数
,试求实数![]() 的值;
的值;
(2)设关于![]() 的方程
的方程![]() 的两个实根为
的两个实根为![]() ;试问:是否存在实数
;试问:是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]() .
.
【解析】
(1)通过求导,判断函数![]() 的单调区间,再由函数最小值列出方程解出
的单调区间,再由函数最小值列出方程解出![]() 的值;(2)化简
的值;(2)化简![]() ,利用韦达定理求出
,利用韦达定理求出![]() ,则问题等价于:是否存在实数
,则问题等价于:是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立,设
恒成立,设![]()
![]() ,根据
,根据![]() 的范围可得
的范围可得![]() 的最大值,代入不等式,将其看作关于
的最大值,代入不等式,将其看作关于![]() 的一次函数,再讨论求出
的一次函数,再讨论求出![]() 的取值范围即得.
的取值范围即得.
(1)由题![]() ,
,![]() ,
,
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 是单调递增,故
是单调递增,故![]() ,解得:
,解得:![]() .
.
当![]() 时,
时,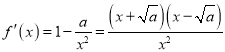 ,
,![]() 在区间
在区间![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
则![]() 在
在![]() 处取得最小值,故
处取得最小值,故![]() ,
,![]() ,无解.
,无解.
综上,![]() .
.
(2)由题得,![]() ,化简整理得
,化简整理得![]() .
.
![]() ,
,![]() 方程
方程![]() 有两个非零实根
有两个非零实根![]() ,
,
可得![]() ,则有
,则有![]() =
=![]() =
=![]() ,
,
本题等价于是否存在![]() ,使不等式
,使不等式
![]()
![]() ——①
——①
对任意![]() ,
,![]() 恒成立.
恒成立.
把![]() 看作关于
看作关于![]() 的函数
的函数![]()
![]() ,则①式等价于
,则①式等价于
![]()
![]() ——②
——②
![]() ,
,![]()
![]()
![]() ,从而②式转化为
,从而②式转化为
![]() 3,
3,
即![]() ——③
——③
对![]() 恒成立,
恒成立,
把③式的左边看作![]() 的函数,记
的函数,记![]()
![]() =
=![]() ,
,
若![]() ,③式显然不成立;
,③式显然不成立;
若![]() ,
,![]() 是
是![]() 的一次函数,要使
的一次函数,要使![]() 对
对![]() 恒成立,只要
恒成立,只要![]() 和
和![]() 同时成立即可,解不等式组
同时成立即可,解不等式组
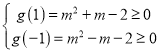 ,
,
得![]() 或
或![]() .
.
故存在实数![]() ,使不等式
,使不等式![]()
![]() 对任意
对任意![]() ,
,![]() 恒成立,其取值范围是
恒成立,其取值范围是![]() 或
或![]() .
.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=![]() ;(2)A(A∩B).
;(2)A(A∩B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用清水漂洗衣服上残留的洗衣液,对用一定量的清水漂洗一次的效果作如下假定:用1个单位量的水可洗掉衣服上残留洗衣液质量的一般,用水越多漂洗效果越好,但总还有洗衣液残留在衣服上.设用![]() 单位量的清水漂洗一次后,衣服上残留的洗衣液质量与本次漂洗前残留的洗衣液质量之比为函数
单位量的清水漂洗一次后,衣服上残留的洗衣液质量与本次漂洗前残留的洗衣液质量之比为函数![]() ,其中
,其中![]() .
.
(1)试规定![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)根据假定写出函数![]() 应该满足的条件和具有的性质,并写出满足假定的一个指数函数;
应该满足的条件和具有的性质,并写出满足假定的一个指数函数;
(3)设函数![]() .现有
.现有![]() (
(![]() )单位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗两次,试确定哪种方式漂洗效果更好?并说明理由.
)单位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗两次,试确定哪种方式漂洗效果更好?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
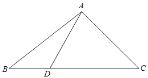
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线![]() 上,且圆C与x轴交于两点
上,且圆C与x轴交于两点![]() ,
,![]() .
.
(1)求圆C的方程;
(2)已知圆M:![]() ,设
,设![]() 为坐标平面上一点,且满足:存在过点
为坐标平面上一点,且满足:存在过点![]() 且互相垂直的直线
且互相垂直的直线![]() 和
和![]() 有无数对,它们分别与圆C和圆M相交,且圆心C到直线
有无数对,它们分别与圆C和圆M相交,且圆心C到直线![]() 的距离是圆心M到直线
的距离是圆心M到直线![]() 的距离的2倍,试求所有满足条件的点
的距离的2倍,试求所有满足条件的点![]() 的坐标
的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() ,
,![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;
恒成立;![]() :当
:当![]() 时,
时,![]() 是单调函数.如果满足
是单调函数.如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足
,满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,求
,求![]() (
(![]() 为全集).
为全集).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com