
【题目】(本小题满分13分)如图,三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
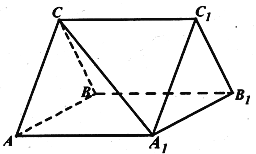
(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明详见解析;(2)1.
【解析】
试题分析:本题主要考查线线垂直、线面垂直、三棱锥的体积等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力.第一问,在等腰三角形中,O为AB中点,所以CO为高,由已知可得![]() 为等边三角形,所以得到
为等边三角形,所以得到![]() ,所以利用线面垂直的判定得
,所以利用线面垂直的判定得![]() 平面
平面![]() ,最后利用线面垂直的性质得
,最后利用线面垂直的性质得![]() ;第二问,在等边
;第二问,在等边![]() 和
和![]() 中,先解出CO和
中,先解出CO和![]() 的长,判断得出
的长,判断得出![]() 是直角三角形,所以得证
是直角三角形,所以得证![]() 平面
平面![]() ,再利用三棱锥的体积公式计算即可.
,再利用三棱锥的体积公式计算即可.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
![]() ,故
,故![]() , 2分
, 2分
又![]() ,
,![]() .
.
![]() 为等边三角形.
为等边三角形.
![]() , 4分
, 4分
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() 平面
平面![]() . 6分
. 6分
又![]() 平面
平面![]() ,因此
,因此![]() ; 7分
; 7分
(2)解:在等边![]() 中
中![]() ,在等边
,在等边![]() 中
中![]() ;
;
在![]() 中
中![]() .
.
![]()
![]() 是直角三角形,且
是直角三角形,且![]() ,故
,故![]() . 9分
. 9分
又![]() 、
、![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() .
.
故![]() 是三棱锥
是三棱锥![]() 的高. 10分
的高. 10分
又![]() .
.
![]() 三棱锥
三棱锥![]() .
.
![]() 三棱锥
三棱锥![]() 的体积为1. 13分
的体积为1. 13分


科目:高中数学 来源: 题型:
【题目】在一次水下考古活动中,某一潜水员需潜水50米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.3升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升;潜水员在此次考古活动中的总用氧量为
米/分钟,每分钟用氧量为0.32升;潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是10分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气13.5升,请问潜水员最多在水下多少分钟(结果取整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆M: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆M有两个不同的交点P,Q,l与矩形ABCD有两个不同的交点S,T.求 ![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.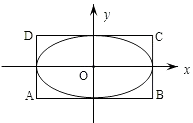
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是定义在(﹣∞,+∞)上的奇函数,且满足
是定义在(﹣∞,+∞)上的奇函数,且满足 ![]()
(1)求实数a,b,并确定函数f(x)的解析式
(2)用定义证明f(x)在(﹣1,1)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x+2)的定义域为(0,2),则函数y=f(log2x)的定义域为( )
A.(﹣∞,1)
B.(1,4)
C.(4,16)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: (![]() >b>0)的离心率为
>b>0)的离心率为![]() ,A(
,A(![]() ,0), B(0,b),O(0,0),△OAB的面积为1.
,0), B(0,b),O(0,0),△OAB的面积为1.
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN|·|BM|为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com