
【题目】已知![]() (x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(1)求数列{an}的第n+1项;
(2)若![]() 是
是![]() ,
,![]() 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
【答案】(1) an+1=6n+3(2) ![]()
【解析】
试题分析:(1)有![]() (x≥0)成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;(2)由于
(x≥0)成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;(2)由于![]() 是
是![]() ,
,![]() 的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn
的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn
试题解析:因为![]() ,
,![]() ,
,![]() (x≥0)成等差数列,所以
(x≥0)成等差数列,所以![]() ×2=
×2=![]() +
+![]() .
.
所以f(x)=(![]() +
+![]() )2.
)2.
因为Sn=f(Sn-1)(n≥2),
所以Sn=f(Sn-1)=(![]() +
+![]() )2.
)2.
所以![]() =
=![]() +
+![]() ,
,![]() -
-![]() =
=![]() .
.
所以{![]() }是以
}是以![]() 为公差的等差数列.
为公差的等差数列.
因为a1=3,所以S1=a1=3.
所以![]() =
=![]() +(n-1)
+(n-1) ![]() =
=![]() +
+![]() -
-![]() =
=![]() n.
n.
所以Sn=3n2(n∈N*).所以an+1=Sn+1-Sn=3(n+1)2-3n2=6n+3.
(2)因为数列![]() 是
是![]() ,
,![]() 的等比中项,
的等比中项,
所以(![]() )2=
)2=![]() ·
·![]() ,
,
所以bn=![]() =
=![]() =
=![]() .
.
所以Tn=b1+b2+…+bn=![]()


科目:高中数学 来源: 题型:
【题目】下列关于四种命题的真假判断正确的是( )
A. 原命题与其逆否命题的真值相同 B. 原命题与其逆命题的真值相同
C. 原命题与其否命题的真值相同 D. 原命题的逆命题与否命题的真值相反
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的倾斜角为45°,以坐标原点为极点,
的倾斜角为45°,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的交点为点
的交点为点![]() .
.
(1)求直线![]() 的参数方程;
的参数方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() 两点,
两点,![]() .
.
(1)求证:![]() 为定值;
为定值;
(2)是否存在平行于![]() 轴的定直线被以
轴的定直线被以![]() 为直径的圆截得的弦长为定值?如果存在,求该直线方程和弦长;如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求该直线方程和弦长;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置, 指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右下表.
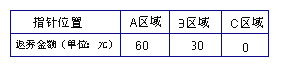

例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)已知顾客甲消费后获得![]() 次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为
次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为![]() ,每次转动转盘的结果相互独立,设
,每次转动转盘的结果相互独立,设![]() 为顾客甲转动转盘指针落在区域边界的次数,
为顾客甲转动转盘指针落在区域边界的次数,![]() 的数学期望
的数学期望![]() ,方差
,方差![]() .求
.求![]() 、
、![]() 的值;
的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() ,如图2,将
,如图2,将![]() ,
, ![]() 分别沿
分别沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,设
,设![]() 为
为![]() 上任意一点.
上任意一点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com