
【题目】为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高![]() 和体重
和体重![]() 数据如下表所示:
数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 164 | 160 | 158 | 172 | 162 | 164 | 174 | 166 |
体重 | 60 | 46 | 43 | 48 | 48 | 50 | 61 | 52 |
该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.

(1)调查员甲计算得出该组数据的线性回归方程为![]() ,请你据此预报一名身高为
,请你据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: .
.
【答案】(1)一名身高为![]() 的女大学生的体重约为
的女大学生的体重约为![]() (2)回归方程为
(2)回归方程为![]() ,一名身高为
,一名身高为![]() 的女大学生的体重约为
的女大学生的体重约为![]() (3)乙的模型得到的预测值更可靠,详见解析
(3)乙的模型得到的预测值更可靠,详见解析
【解析】
(1)计算平均数,求出![]() ,即可求出回归方程;把178代入即可求出
,即可求出回归方程;把178代入即可求出![]() 的女大学生的体重;
的女大学生的体重;
(2)根据余下的数据计算平均数,求出![]() ,
,![]() ,即可求出回归方程;代入公式,即可求出身高为
,即可求出回归方程;代入公式,即可求出身高为![]() 的女大学生的体重;
的女大学生的体重;
(3)从散点图以及计算数据两个方面来分析甲和乙谁的方程可靠.
解:(1)经计算:![]() ,
,
于是:![]() ,
,
则该组数据的线性回归方程为![]() ,
,
当![]() 时,
时,![]() ,
,
于是:一名身高为![]() 的女大学生的体重约为
的女大学生的体重约为![]() ;
;
(2)按照调查人员乙的想法,剩下的数据如下表所示:
编号 | 2 | 3 | 5 | 6 | 7 | 8 |
身高 | 160 | 158 | 162 | 164 | 174 | 166 |
体重 | 46 | 43 | 48 | 50 | 61 | 52 |
经计算:![]() ,
,
于是:
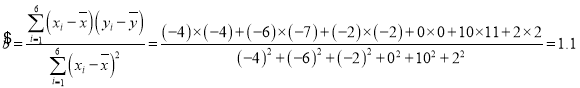
![]() ,
,
则该组数据的线性回归方程为![]() ,
,
当![]() 时,
时,![]() ,
,
于是:一名身高为![]() 的女大学生的体重约为
的女大学生的体重约为![]() ;
;
(3)乙的模型得到的预测值更可靠,
理由如下:①从散点图可以看出,第一组数据和第四组数据确实偏差较大,为更准确的刻画变化趋势,有必要把这两个数据剔除掉;
②从计算结果来看,相对于第七组数据![]() 的女大学生体重,甲对身高
的女大学生体重,甲对身高![]() 的女大学生的预测值明显偏低,而利用乙的回归方程得到的预测值增幅较合理.
的女大学生的预测值明显偏低,而利用乙的回归方程得到的预测值增幅较合理.
(以上给出了两种理由,考生答出其中任意一种或其他合理理由均可得分)


科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
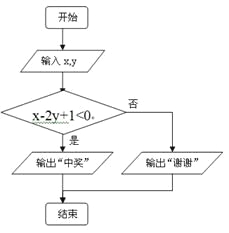
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小威初三参加某高中学校的数学自主招生考试,这次考试由十道选择题组成.得分要求是:做对一道题得![]() 分,做错一道题扣去
分,做错一道题扣去![]() 分,不做得
分,不做得![]() 分,总得分
分,总得分![]() 分就算及格.小威的目标是至少得
分就算及格.小威的目标是至少得![]() 分获得及格.在这次考试中,小威确定他做的前六题全对,记
分获得及格.在这次考试中,小威确定他做的前六题全对,记![]() 分;而他做余下的四道题中每道题做对的概率均为
分;而他做余下的四道题中每道题做对的概率均为![]() .考试中,小威思量:从余下的四道题中再做一道并且及格的概率
.考试中,小威思量:从余下的四道题中再做一道并且及格的概率![]() ;从余下的四道题中恰做两道并且及格的概率
;从余下的四道题中恰做两道并且及格的概率![]() .他发现
.他发现![]() ,只做一道更容易及格.
,只做一道更容易及格.
(1)求:小威从余下的四道题中恰做三道并且及格的概率![]() ,从余下的四道题中全做并且及格的概率
,从余下的四道题中全做并且及格的概率![]() ,求
,求![]() 及
及![]() ;
;
(2)由于![]() 的大小影响,请你帮小威讨论:小威从余下的四道题中恰做几道并且及格的概率最大?
的大小影响,请你帮小威讨论:小威从余下的四道题中恰做几道并且及格的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 的最小值为
的最小值为![]() ,且该椭圆的离心率为
,且该椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上不同的两点,且
上不同的两点,且![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是实系数一元二次方程
是实系数一元二次方程![]() 的虚根,记它在直角坐标平面上的对应点位
的虚根,记它在直角坐标平面上的对应点位![]() .
.
(1)若![]() 在直线
在直线![]() 上,求证:
上,求证:![]() 在圆
在圆![]() :
:![]() 上;
上;
(2)给定圆![]() ,则存在唯一的线段
,则存在唯一的线段![]() 满足:
满足:
①若![]() 在圆
在圆![]() 上,则
上,则![]() 在线段
在线段![]() 上;
上;
②若![]() 是线段
是线段![]() 上一点(非端点),则
上一点(非端点),则![]() 在圆
在圆![]() 上,写出线段
上,写出线段![]() 的表达式,并说明理由;
的表达式,并说明理由;
(3)由(2)知线段![]() 与圆
与圆![]() 之间确定了一种对应关系,通过这种对应关系的研究,填写表一(表中
之间确定了一种对应关系,通过这种对应关系的研究,填写表一(表中![]() 是(1)中圆
是(1)中圆![]() 的对应线段).
的对应线段).
表一:
线段 |
|
| |
| |
线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:
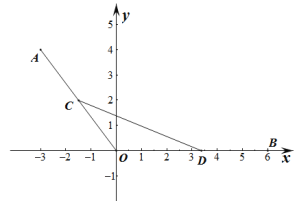
【题目】如图,在平面直角坐标系![]() 中,己知点
中,己知点![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,满足
上的动点,满足![]() .
.
(1)若![]() 点恰好与
点恰好与![]() 点重合,求半径为
点重合,求半径为![]() 且与直线
且与直线![]() 相切于
相切于![]() 点的圆的方程;
点的圆的方程;
(2)设![]() ,求证:
,求证:![]() 的外接圆恒过定点(异于原点).
的外接圆恒过定点(异于原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com