
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 的最小值为
的最小值为![]() ,且该椭圆的离心率为
,且该椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上不同的两点,且
上不同的两点,且![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
是否经过一个定点?若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 过定点
过定点![]()
【解析】
(1)依题意得到方程组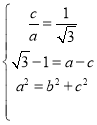 解得;
解得;
(2)已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,因为
轴上,因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,列出韦达定理,由直线
,联立直线与椭圆方程,列出韦达定理,由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,令
,令![]() ,计算其横坐标是否为定值.
,计算其横坐标是否为定值.
解:(1)依题意得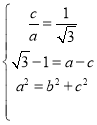 ,解得
,解得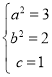 ,所以椭圆
,所以椭圆![]() ;
;
(2)直线![]() 过定点
过定点![]() ,
,
证明:已知![]() 且
且![]() ,可知点
,可知点![]() 同在
同在![]() 轴的上方或下方,
轴的上方或下方,
由对称性可知,若动直线![]() 经过一个定点,则该定点在
经过一个定点,则该定点在![]() 轴上,
轴上,
因为![]() ,所以点
,所以点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立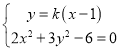 ,消去
,消去![]() 整理得
整理得![]() 又
又![]() ,
,
所以 ,
,
由直线![]() 的斜率
的斜率![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得:
,得:![]() ,
,
由![]() ,
,
所以![]()
即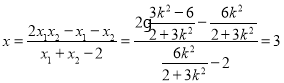 ,
,
所以直线![]() 过定点
过定点![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),把曲线
为参数),把曲线![]() 横坐标缩短为原来的
横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() ,直线
,直线![]() 的普通方程是
的普通方程是![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系;
轴正半轴为极轴建立极坐标系;
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空有限集合![]() 是由若干个正实数组成,集合
是由若干个正实数组成,集合![]() 的元素个数
的元素个数![]() .对于任意
.对于任意![]() ,数
,数![]() 或
或![]() 中至少有一个属于
中至少有一个属于![]() ,称集合
,称集合![]() 是“好集”:否则,称集合
是“好集”:否则,称集合![]() 是“坏集”.
是“坏集”.
(1)判断![]() 和
和![]() 是“好集”,还是“坏集”;
是“好集”,还是“坏集”;
(2)题设的有限集合![]() 中,既有大于1的元素,又有小于1的元素,证明:集合
中,既有大于1的元素,又有小于1的元素,证明:集合![]() 是“坏集”.
是“坏集”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高![]() 和体重
和体重![]() 数据如下表所示:
数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 164 | 160 | 158 | 172 | 162 | 164 | 174 | 166 |
体重 | 60 | 46 | 43 | 48 | 48 | 50 | 61 | 52 |
该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.

(1)调查员甲计算得出该组数据的线性回归方程为![]() ,请你据此预报一名身高为
,请你据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条形图给出的是2017年全年及2018年全年全国居民人均可支配收入的平均数与中位数,饼图给出的是2018年全年全国居民人均消费及其构成,现有如下说法:
①2018年全年全国居民人均可支配收入的平均数的增长率低于2017年;
②2018年全年全国居民人均可支配收入的中位数约是平均数的![]() ;
;
③2018年全年全国居民衣(衣着)食(食品烟酒)住(居住)行(交通通信)的支出超过人均消费的![]() .
.
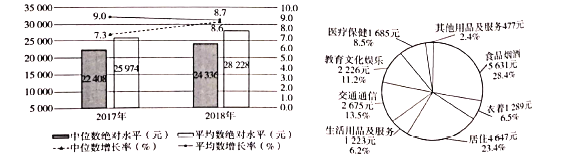
则上述说法中,正确的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直平行六面体![]() 的所有棱长都为2,
的所有棱长都为2,![]() ,过体对角线
,过体对角线![]() 的截面S与棱
的截面S与棱![]() 和
和![]() 分别交于点E、F,给出下列命题中:
分别交于点E、F,给出下列命题中:
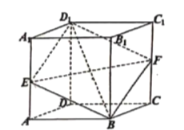
①四边形![]() 的面积最小值为
的面积最小值为![]() ;
;
②直线EF与平面![]() 所成角的最大值为
所成角的最大值为![]() ;
;
③四棱锥![]() 的体积为定值;
的体积为定值;
④点![]() 到截面S的距离的最小值为
到截面S的距离的最小值为![]() .
.
其中,所有真命题的序号为( )
A.①②③B.①③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车.每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车.今年初投入了电力型公交车120辆,混合动力型公交车300辆,计划以后电力型车每年的投入量比上一年增加![]() ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入![]() 辆.设
辆.设![]() ,
,![]() 分别为第
分别为第![]() 年投入的电力型公交车,混合动力型公交车的数量,设
年投入的电力型公交车,混合动力型公交车的数量,设![]() ,
,![]() 分别为
分别为![]() 年里投入的电力型公交车,混合动力型公交车的总数量.
年里投入的电力型公交车,混合动力型公交车的总数量.
(1)求![]() ,
,![]() ,并求
,并求![]() 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数![]() ;
;
(2)该市计划用8年的时间完成全部更换,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com