
【题目】甲、乙两位同学分别做下面这道题目:在平面直角坐标系中,动点![]() 到
到![]() 的距离比
的距离比![]() 到
到![]() 轴的距离大
轴的距离大![]() ,求
,求![]() 的轨迹.甲同学的解法是:解:设
的轨迹.甲同学的解法是:解:设![]() 的坐标是
的坐标是![]() ,则根据题意可知
,则根据题意可知
![]() ,化简得
,化简得![]() ; ①当
; ①当![]() 时,方程可变为
时,方程可变为![]() ;②这表示的是端点在原点、方向为
;②这表示的是端点在原点、方向为![]() 轴正方向的射线,且不包括原点; ③当
轴正方向的射线,且不包括原点; ③当![]() 时,方程可变为
时,方程可变为![]() ; ④这表示以
; ④这表示以![]() 为焦点,以直线
为焦点,以直线![]() 为准线的抛物线;⑤所以
为准线的抛物线;⑤所以![]() 的轨迹为端点在原点、方向为
的轨迹为端点在原点、方向为![]() 轴正方向的射线,且不包括原点和以
轴正方向的射线,且不包括原点和以![]() 为焦点,以直线
为焦点,以直线![]() 为准线的抛物线. 乙同学的解法是:解:因为动点
为准线的抛物线. 乙同学的解法是:解:因为动点![]() 到
到![]() 的距离比
的距离比![]() 到
到![]() 轴的距离大
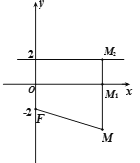
轴的距离大![]() . ①如图,过点
. ①如图,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() . 则
. 则![]() .设直线
.设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,则
,则![]() ; ②即动点
; ②即动点![]() 到直线
到直线![]() 的距离比
的距离比![]() 到
到![]() 轴的距离大
轴的距离大![]() ; ③所以动点
; ③所以动点![]() 到
到![]() 的距离与
的距离与![]() 到直线
到直线![]() 的距离相等;④所以动点
的距离相等;④所以动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以直线
为焦点,以直线![]() 为准线的抛物线; ⑤甲、乙两位同学中解答错误的是________(填“甲”或者“乙”),他的解答过程是从_____处开始出错的(请在横线上填写① 、②、③、④ 或⑤ ).
为准线的抛物线; ⑤甲、乙两位同学中解答错误的是________(填“甲”或者“乙”),他的解答过程是从_____处开始出错的(请在横线上填写① 、②、③、④ 或⑤ ).
科目:高中数学 来源: 题型:
【题目】某海湿地如图所示,A、B和C、D分别是以点O为中心在东西方向和南北方向设置的四个观测点,它们到点O的距离均为![]() 公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
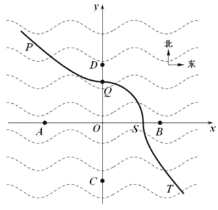
(1)求观光长廊PQST所在的曲线的方程;
(2)在观光长廊的PQ段上,需建一服务站M,使其到观测点A的距离最近,问如何设置服务站M的位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinπx,g(x)=x2﹣x+2,则( )
A. 曲线y=f(x)+g(x)不是轴对称图形
B. 曲线y=f(x)﹣g(x)是中心对称图形
C. 函数y=f(x)g(x)是周期函数
D. 函数![]() 最大值为
最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为F1,F2,离心率为
的左右焦点分别为F1,F2,离心率为![]() ,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
,设过点F2的直线l被椭圆C截得的线段为MN,当l⊥x轴时,|MN|=3.
(1)求椭圆C的标准方程;
(2)在x轴上是否存在一点P,使得当l变化时,总有PM与PN所在的直线关于x轴对称?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
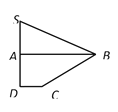
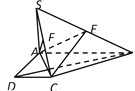
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面是正三角形、侧棱垂直于底面的三棱柱ABC﹣A1B1C1中,底面边长为a,侧棱长为2a,点M是A1B1的中点.
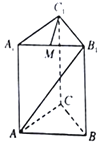
(1)证明:MC1⊥AB1.
(2)求直线AC1与侧面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com