
【题目】今年3月5日,国务院总理李克强作的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”.教育部日前公布的《教育部2019年部门预算》中透露,2019年教育部拟抽检博士学位论文约6000篇,预算为800万元.国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定:每篇抽检的学位论文送3位同行专家进行评议,3位专家中有2位以上(含2位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”.有且只有1位专家评议意见为“不合格”的学位论文,将再送2位同行专家进得复评,2位复评专家中有1位以上(含1位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”.设每篇学位论文被每位专家评议为“不合格”的概率均为![]() ,且各篇学位论文是否被评议为“不合格”相互独立.
,且各篇学位论文是否被评议为“不合格”相互独立.
(1)记一篇抽检的学位论文被认定为“存在问题学位论文”的概率为![]() ,求
,求![]() ;
;
(2)若拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的评审费用为1500元;除评审费外,其它费用总计为100万元.现以此方案实施,且抽检论文为6000篇,问是否会超过预算?并说明理由.
【答案】(1)![]() ;(2)若以此方案实施,不会超过预算.
;(2)若以此方案实施,不会超过预算.
【解析】
(1)先求出一篇学位论文初评被认定为“存在问题学位论文”的概率,再求出一篇学位论文复评被认定为“存在问题学位论文”的概率,再把它们相加即得解;(2)先求出![]()
![]() ,再求出其最大值,比较最大值和预算的大小即得解.
,再求出其最大值,比较最大值和预算的大小即得解.
(1)因为一篇学位论文初评被认定为“存在问题学位论文”的概率为![]() ,
,
一篇学位论文复评被认定为“存在问题学位论文”的概率为![]() ,
,
所以一篇学位论文被认定为“存在问题学位论文”的概率为
![]()
![]()
![]() .
.
(2)设每篇学位论文的评审费为![]() 元,则
元,则![]() 的可能取值为900,1500.
的可能取值为900,1500.
![]() ,
, ![]() ,
,
所以![]()
![]() .
.
令![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
所以![]() 的最大值为
的最大值为![]() .
.
所以实施此方案,最高费用为![]() (万元).
(万元).
综上,若以此方案实施,不会超过预算.


科目:高中数学 来源: 题型:
【题目】以下说法正确的是( )
A.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
B.命题“![]() ,
,![]() 互为倒数,则
互为倒数,则![]() ”的逆命题为真
”的逆命题为真
C.命题“若![]() ,
,![]() 都是偶数,则
都是偶数,则![]() 是偶数”的否命题为真
是偶数”的否命题为真
D.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为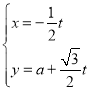 (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(Ⅱ)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.

(1)证明:无论点E怎样运动,四边形EFD1D都为矩形;
(2)当EC=1时,求几何体A﹣EFD1D的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com