
已知函数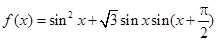 .
.
(1)求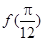 的值;
的值;
(2)当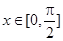 时,求函数
时,求函数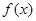 的最大值和最小值.
的最大值和最小值.
(1)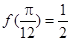 ;(2)最小值
;(2)最小值 ,最大值
,最大值 .
.
解析试题分析:本题主要考查诱导公式、倍角公式、降幂公式、两角和与差的正弦公式、三角函数最值等基础知识,考查学生的分析问题解决问题的能力、运用数学公式计算的能力,考查学生的数形结合思想.第一问,先利用诱导公式、倍角公式、降幂公式、两角和与差的正弦公式化简表达式,使之化简为 的形式,再将
的形式,再将 代入求三角函数值;第二问,将已知x的范围代入第一问化简的表达式中,求出角
代入求三角函数值;第二问,将已知x的范围代入第一问化简的表达式中,求出角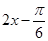 的范围,再数形结合得到最大值和最小值.
的范围,再数形结合得到最大值和最小值.
(1)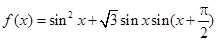
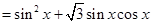
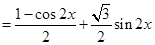
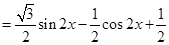
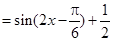 .
.
所以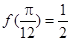 . 7分
. 7分
(2)当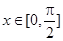 时,
时,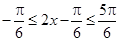 .
.
所以,当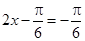 时,即
时,即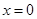 时,函数
时,函数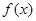 取得最小值
取得最小值 ;
;
当 时,即
时,即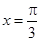 时,函数
时,函数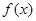 取得最大值
取得最大值 . 13分
. 13分
考点:诱导公式、倍角公式、降幂公式、两角和与差的正弦公式、三角函数最值.


科目:高中数学 来源: 题型:解答题
如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm,周期为3 s,且物体向右运动到A点(距平衡位置最远处)开始计时.(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;(2)求该物体在t=5 s时的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系中,角 和角
和角 的终边分别与单位圆交于
的终边分别与单位圆交于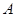 ,
, 两点,(其中
两点,(其中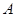 为第一象限点,
为第一象限点, 为第二象限点)
为第二象限点)
(1)若点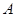 的横坐标是
的横坐标是 ,点
,点 的纵坐标是
的纵坐标是 ,求
,求 的值;
的值;
(2)若 , 求
, 求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•广东)已知函数f(x)=2sin( x﹣
x﹣ ),x∈R.
),x∈R.
(1)求f(0)的值;
(2)设α,β∈ ,f(3
,f(3 )=
)=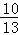 ,f(3β+
,f(3β+ )=
)= .求sin(α+β)的值.
.求sin(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数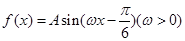 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是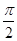 ,且满足,
,且满足,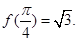
(1)求 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,sinB= ,求△ABC的面积。
,求△ABC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com