
【题目】记函数f(x)=log2(2x﹣3)的定义域为集合M,函数g(x)=![]() 的定义域为集合N.求:
的定义域为集合N.求:
(Ⅰ)集合M,N;
(Ⅱ)集合M∩N,R(M∪N).
【答案】解:(1)由2x﹣3>0 得 x>![]() ,∴M={x|x>
,∴M={x|x>![]() }.
}.
由(x﹣3)(x﹣1)>0 得 x<1 或x>3,∴N={x|x<1,或 x>3}.
(2)M∩N=(3,+∞),M∪N={x|x<1,或 x>3},
∴CR(M∪N)=[1 ![]() ].
].
【解析】(1)求函数f(x)的定义域求得M,求函数g(x)的定义域求得N.
(2)根据两个集合的交集的定义求得 M∩N,再根据两个集合的并集的定义求得M∪N,再根据补集的定义求得CR(M∪N).
【考点精析】关于本题考查的交、并、补集的混合运算和对数函数的定义域,需要了解求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法;对数函数的定义域范围:(0,+∞)才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两个容器,甲容器容量为![]() ,装满纯酒精,乙容器容量为
,装满纯酒精,乙容器容量为![]() ,其中装有体积为
,其中装有体积为![]() 的水(
的水(![]() :单位:
:单位: ![]() ).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过
).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过![]() 次操作之后,乙容器中含有纯酒精
次操作之后,乙容器中含有纯酒精![]() (单位:
(单位: ![]() ),下列关于数列
),下列关于数列![]() 的说法正确的是( )
的说法正确的是( )
A. 当![]() 时,数列
时,数列![]() 有最大值
有最大值![]()
B. 设![]() ,则数列
,则数列![]() 为递减数列
为递减数列
C. 对任意的![]() ,始终有
,始终有![]()
D. 对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,设动点
为坐标原点,设动点![]() .
.
(1)当![]() 时,若过点
时,若过点![]() 的直线
的直线![]() 与圆
与圆![]() :
:![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)当![]() 时,求以
时,求以![]() 为直径且被直线
为直径且被直线![]() 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)当![]() 时,设
时,设![]() ,过点
,过点![]() 作
作![]() 的垂线,与以
的垂线,与以![]() 为直径的圆交于点
为直径的圆交于点![]() ,垂足为
,垂足为![]() ,试问:线段
,试问:线段![]() 的长是否为定值?若为定值,求出这个定值;若不为定值,请说明理由.
的长是否为定值?若为定值,求出这个定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)若对任意的实数![]() ,函数
,函数![]() (
(![]() 为实常数)的图象与函数
为实常数)的图象与函数![]() 的图象总相切于一个定点.
的图象总相切于一个定点.
① 求![]() 与
与![]() 的值;
的值;
② 对![]() 上的任意实数
上的任意实数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
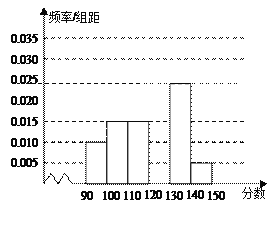
【题目】某校从参加高二某次月考的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组![]() 后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
(Ⅰ)求分数在![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在分数段![]() 的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段
的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段![]() 内的概率。
内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣![]() 或﹣
或﹣![]()
B.﹣![]() 或﹣
或﹣![]()
C.﹣![]() 或﹣
或﹣![]()
D.﹣![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
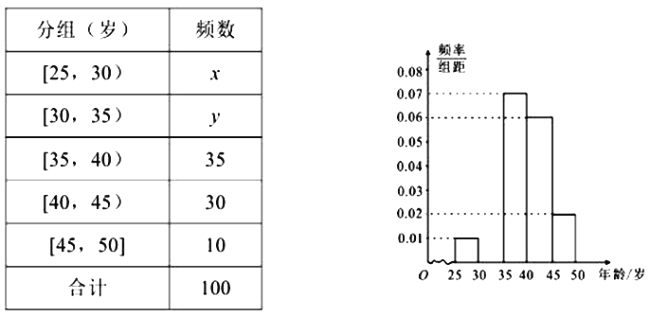
(Ⅰ)求频率分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人中随机选取2人各赠送精美礼品一份,设这2名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com