
【题目】已知等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,数列{an}满足a2=4b1,nbn+1-(n+1)bn=n2+n,(n∈N*).
(1)求数列{an}的通项公式;
(2)证明数列{![]() }为等差数列;
}为等差数列;
(3)设数列{cn}的通项公式为:Cn=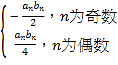 ,其前n项和为Tn,求T2n.
,其前n项和为Tn,求T2n.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)由等比数列的基本量法求解;
(2)求得![]() ,再证
,再证![]() 为常数即可;
为常数即可;
(3)先并项,设![]() ,然后有
,然后有![]() ,用错位相减法计算.
,用错位相减法计算.
(1)由于等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,
所以S3-S2=a4-2a2=a3,
整理得![]() ,
,
由于a2≠0,
所以q2-q-2=0,由于q>0,
解得q=2.
由于a1+a2=2a2-2,解得a1=2,
所以![]() .
.
(2)数列{an}满足a2=4b1,解得b1=1,
由于nbn+1-(n+1)bn=n2+n,
所以![]() (常数).
(常数).
所以数列数列{![]() }是以1为首项1为公差的等差数列.
}是以1为首项1为公差的等差数列.
(3)由于数列数列{![]() }是以1为首项1为公差的等差数列.
}是以1为首项1为公差的等差数列.
所以![]() ,解得
,解得![]()
由于数列{cn}的通项公式为:Cn=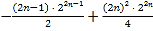 ,
,
所以令![]() =
=![]() =(4n-1)
=(4n-1)![]() 4n-1.
4n-1.
所以![]() ①,
①,
4![]() ②,
②,
①-②得:![]() -(4n-1)
-(4n-1)![]() 4n,
4n,
整理得![]() ,
,
故:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题.
(1)根据以上数据完成下列2×2列联表;
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?
参考公式: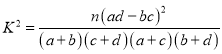 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2,AB=1,E为AD中点,F为CC1中点.
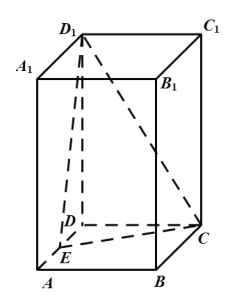
(1)求证:AD⊥D1F;
(2)求证:CE//平面AD1F;
(3)求AA1与平面AD1F成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
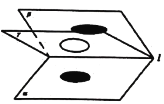
【题目】如图,![]() ,
,![]() ,
,![]() 是由直线
是由直线![]() 引出的三个不重合的半平面,其中二面角
引出的三个不重合的半平面,其中二面角![]() 大小为60°,
大小为60°,![]() 在二面角
在二面角![]() 内绕直线
内绕直线![]() 旋转,圆
旋转,圆![]() 在
在![]() 内,且圆
内,且圆![]() 在
在![]() ,
,![]() 内的射影分别为椭圆
内的射影分别为椭圆![]() ,
,![]() .记椭圆
.记椭圆![]() ,
,![]() 的离心率分别为
的离心率分别为![]() ,
,![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共14分)
如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]()
(Ⅱ)若![]() 求
求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面![]() 与平面
与平面![]() 垂直时,求
垂直时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在坐标原点,焦点
的中心在坐标原点,焦点![]() 在
在![]() 轴上,过坐标原点的直线
轴上,过坐标原点的直线![]() 交
交![]() 于
于![]() 两点,
两点,![]() ,
,![]() 面积的最大值为
面积的最大值为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆上与
是椭圆上与![]() 不重合的一点,证明:直线
不重合的一点,证明:直线![]() 的斜率之积为定值;
的斜率之积为定值;
(3)当点![]() 在第一象限时,
在第一象限时,![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线![]() 的参数方程为
的参数方程为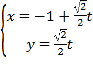 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线C交于
与曲线C交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com