
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
【答案】(1)数列![]() 的公比为1(2)①
的公比为1(2)①![]() ②存在;s,t的值为
②存在;s,t的值为![]() 和
和![]()
【解析】
(1)由![]() 得
得![]() 的等式,再由
的等式,再由![]() 可求得
可求得![]() 的关系,得出结论;
的关系,得出结论;
(2)①已知条件可变形为![]() (
(![]() ),从而可求出
),从而可求出![]() ,从而可得
,从而可得![]() ,注意
,注意![]() ,求积可得
,求积可得![]() ;
;
②由①知![]() .利用导数研究函数
.利用导数研究函数![]() 的单调性得数列
的单调性得数列![]() 的单调性:
的单调性:![]() ,假设存在s,t满足题意,若
,假设存在s,t满足题意,若![]() ,由单调性出现矛盾,这样
,由单调性出现矛盾,这样![]() ,
,![]() ,分别求
,分别求![]() .即可得结论.
.即可得结论.
(1)因为数列![]() 为等差数列,
为等差数列,
所以![]() .
.
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() (*)
(*)
因为数列![]() 为等比数列,所以
为等比数列,所以![]() ,
,
代入(*)得![]() ,即
,即![]() ,
,
所以![]() ,
,
故数列![]() 的公比为1.
的公比为1.
(2)①当![]() 时,由
时,由![]()
得![]() ,
,
从而![]()
又因为![]() ,
,![]() ,
,
所以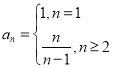
故![]() ,
,![]() ,
,
所以![]() .
.
综上,数列![]() 的通项公式为
的通项公式为![]() .
.
②由①知![]() .
.
记![]() ,则
,则![]() ,
,
从而函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又因为![]() ,
,
所以![]() .
.
假设存在s,t满足题意,若![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,不合题意,
,不合题意,
所以s只能为2,4,6,且![]() .
.
(i)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
故![]() .
.
由数列![]() 的单调性可知存在唯一的
的单调性可知存在唯一的![]() 满足题意.
满足题意.
(ii)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
故![]() .
.
同(i)知![]() .
.
(ⅲ)当![]() 时,由
时,由![]() ,得
,得![]()
故![]() .
.
又因为![]() ,
,
由数列![]() 的单调性知
的单调性知![]() ,故
,故![]() ,
,
但![]() 不成立,所以与题意不符.
不成立,所以与题意不符.
综上,满足条件的s,t的值为![]() 和
和![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过抛物线的焦点
,过抛物线的焦点![]() 且与
且与![]() 轴垂直的直线与抛物线在第一象限交于点
轴垂直的直线与抛物线在第一象限交于点![]() ,
,![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求抛物线的标准方程;
(2)若![]() ,
,![]() ,
,![]() 为抛物线上的两个不同的点,直线
为抛物线上的两个不同的点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]()
![]() ,求点
,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() 若数列
若数列![]() 满足
满足![]() 其中
其中![]() 则称
则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(I)数列![]() 是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(II)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(III)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() 且
且![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为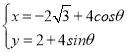 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为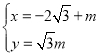 (m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(1)求曲线C的极坐标方程;
(2)直线l与曲线C相交于M,N两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海举办,本届展会共有来自172个国家、地区和国际组织参会,3600多家企业参展,超过40万名采购商到会洽谈采购,其中中国馆更是吸引众人眼球.为了使博览会有序进行,组委会安排6名志愿者到中国馆的某4个展区提供服务,要求![]() 展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
A.156种B.168种C.172种D.180种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数![]() (其中
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )

A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com