
【题目】已知等差数列{an}满足a2=0,a6+a8=﹣10.
(1)求数列{an}的通项公式;
(2)求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
【答案】
(1)解:设等差数列{an}的公差为d,由已知条件可得 ![]() ,
,
解得: ![]() ,
,
故数列{an}的通项公式为an=2﹣n;
(2)解:设数列{ ![]() }的前n项和为Sn,即Sn=a1+
}的前n项和为Sn,即Sn=a1+ ![]() +…+
+…+ ![]() ①,故S1=1,
①,故S1=1,
![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() ②,
②,
当n>1时,①﹣②得:
![]() =a1+
=a1+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]()
=1﹣( ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]()
=1﹣(1﹣ ![]() )﹣
)﹣ ![]() =
= ![]() ,
,
所以Sn= ![]() ,
,
综上,数列{ ![]() }的前n项和Sn=
}的前n项和Sn= ![]()
【解析】(1)根据等差数列的通项公式化简a2=0和a6+a8=﹣10,得到关于首项和公差的方程组,求出方程组的解即可得到数列的首项和公差,根据首项和公差写出数列的通项公式即可;(2)把(1)求出通项公式代入已知数列,列举出各项记作①,然后给两边都除以2得另一个关系式记作②,①﹣②后,利用an的通项公式及等比数列的前n项和的公式化简后,即可得到数列{ ![]() }的前n项和的通项公式.
}的前n项和的通项公式.


科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率. 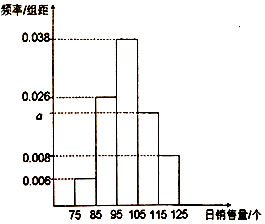
(1)求a的值并估计在一个月(按30天算)内日销售量不低于105个的天数;
(2)利用频率分布直方图估计每天销售量的平均值及方差(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数 ![]() 的导函数
的导函数 ![]() 的图象,对此图象,有如下结论:
的图象,对此图象,有如下结论:
①在区间(-2,1)内 ![]() 是增函数;
是增函数;
②在区间(1,3)内 ![]() 是减函数;
是减函数;
③在 ![]() 时,
时, ![]() 取得极大值;
取得极大值;
④在 ![]() 时,
时, ![]() 取得极小值。
取得极小值。
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤ ![]() )的图象与y轴交于点(0,1).
)的图象与y轴交于点(0,1). 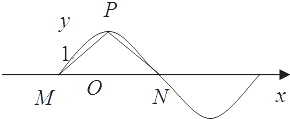
(1)求φ的值.
(2)设P是图象上的最高点,M、N是图象与x轴的交点,求tan∠MPN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com