
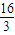



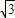
 ,
,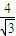 ),可得AB的中垂线方程.再把AB的中垂线方程的y=0,解得x的值,即为所求.
),可得AB的中垂线方程.再把AB的中垂线方程的y=0,解得x的值,即为所求.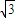 x,把它代入抛物线方程化简可得3x2-8x-16=0,
x,把它代入抛物线方程化简可得3x2-8x-16=0, ,故AB的中点为(
,故AB的中点为( ,
, ),故AB的中垂线方程为 y-
),故AB的中垂线方程为 y- =-
=-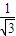 (x-
(x- ).
).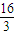 ,故点P的横坐标为
,故点P的横坐标为 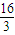 ,即 PF=
,即 PF=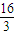 .
.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.8
|
查看答案和解析>>
科目:高中数学 来源:2011年四川省南充市高考数学零诊试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com