练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，底面是平行四边形,平面，，为的中点.

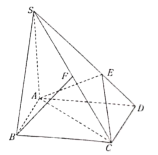
    （I）求证，平面；

    （II）若，求三棱锥的体积.

    【答案】（I）证明见解析；（II）.

    【解析】

    （I）取的中点，连接.连接，交于点，连接交于点，连接.由中位线定理得出为的中点，结合为的中点，得出，由线面平行的判定定理即可求解;

    （II）利用余弦定理得出，结合勾股定理得到，因为四边形是平行四边形，得到DC为三棱锥D-SAC的高，结合，得到，即可求出三棱锥的体积.

    （I）证明：取的中点，连接.连接，交于点，

    连接交于点，连接.

    因为为的中点，是的中点，所以.

    又，所以为的中点，所以为的中点，

    又为的中点，所以.

    因为平面，平面，

    所以平面.

    （II）因为.

    由余弦定理得，

    所以，所以.

    因为平面，所以，

    所以，所以平面.

    因为四边形是平行四边形

    所以DC为三棱锥D-SAC的高

    因为，

    所以,

    即三棱锥的体积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求证：；

    （2）当时，若不等式恒成立，求实数的取值范围；

    （3）若，证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体中，是棱上动点，下列说法正确的是（ ）

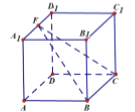
    A. 对任意动点，在平面内不存在与平面平行的直线

    B. 对任意动点，在平面内存在与平面垂直的直线

    C. 当点从运动到的过程中，与平面所成的角变大

    D. 当点从运动到的过程中，点到平面的距离逐渐变小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形ABCD由Rt△ABC和Rt△BCD拼接而成，其中∠BAC＝∠BCD＝90°，∠DBC＝30°，AB＝AC，，将△ABC沿着BC折起，

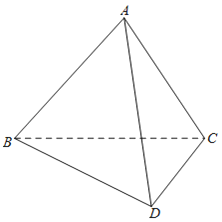
    （1）若，求异面直线AB和CD所成角的余弦值；

    （2）当四面体ABCD的体积最大时，求二面角A﹣BC﹣D的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】顾客请一位工艺师把、两件玉石原料各制成一件工艺品，工艺师带一位徒弟完成这项任务，每件原料先由徒弟完成粗加工，再由工艺师进行精加工完成制作，两件工艺品都完成后交付顾客，两件原料每道工序所需时间（单位：工作日）如下：

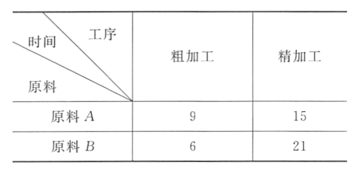
    则最短交货期为_______个工作日．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】重庆近年来旅游业高速发展，有很多著名景点，如洪崖洞、磁器口、朝天门、李子坝等.为了解端午节当日朝天门景点游客年龄的分布情况，从年龄在22～52岁之间的旅游客中随机抽取了1000人，制作了如图的频率分布直方图.

    （1）求抽取的1000人的年龄的平均数、中位数；（每一组的年龄取中间值）

    （2）现从中按照分层抽样抽取8人，再从这8人中随机抽取3人，记这3人中年龄在的人数为，求的分布列及.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）.现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）.

    （1）A类工人中和B类工人中各抽查多少工人？

    （2）从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.

    表一

    生产能力分组

    [100,110)

    [110,120)

    [120,130)

    [130,140)

    [140,150)

    人数

    4

    8

    5

    3

    表二

    生产能力分组

    [110,120)

    [120,130)

    [130,140)

    [140,150)

    人数

    6

    36

    18

    ①先确定再补全下列频率分布直方图（用阴影部分表示）.

    ②就生产能力而言，类工人中个体间的差异程度与类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）

    ③分别估计类工人生产能力的平均数和中位数（求平均数时同一组中的数据用该组区间的中点值作代表）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线.

    (1)若直线不经过第四象限，求的取值范围;

    (2)若直线交轴负半轴于,交轴正半轴于，求的面积的最小值并求此时直线的方程；

    (3)已知点,若点到直线的距离为，求的最大值并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某调研机构，对本地岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，将生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，结果显示，有人为“低碳族”，该人的年龄情况对应的频率分布直方图如图.

    （1）根据频率分布直方图，估计这名“低碳族”年龄的平均值，中位数；

    （2）若在“低碳族”且年龄在、的两组人群中，用分层抽样的方法抽取人，试估算每个年龄段应各抽取多少人？

    查看答案和解析>>

    同步练习册答案