
【题目】已知集合![]() 为集合
为集合![]() 的
的![]() 个非空子集,这
个非空子集,这![]() 个集合满足:①从中任取
个集合满足:①从中任取![]() 个集合都有
个集合都有![]()
![]()
![]() 成立;②从中任取
成立;②从中任取![]() 个集合都有
个集合都有![]()
![]() 成立.
成立.
(Ⅰ)若![]() ,
, ![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() 以及集合
以及集合![]() ;
;
(Ⅲ) 若![]() ,
, ![]() ,求集合
,求集合![]() 中的元素个数的最小值.
中的元素个数的最小值.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】试题分析:(Ⅰ)根据题意一一列举即可;(Ⅱ)根据题意一一列举即可;(Ⅲ)利用反证法进行证明.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅱ)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
(Ⅲ)集合![]() 中元素个数的最小值为120个.
中元素个数的最小值为120个.
下面先证明若![]() ,
,
则![]() ,
, ![]() ,
, ![]()
![]()
![]() .
.
反证法:假设![]() ,不妨设
,不妨设![]() .
.
由假设![]() ,设
,设![]() ,设
,设![]() ,
,
则![]() 是
是![]() 中都没有的元素,
中都没有的元素, ![]() .
.
因为![]() 四个子集的并集为
四个子集的并集为![]() ,
,
所以![]() 与
与![]() 矛盾,所以假设不正确.
矛盾,所以假设不正确.
若![]() ,且
,且![]() ,
, ![]() ,
,
![]()
![]()
![]() 成立.则
成立.则![]() 的
的![]() 个集合的并集共计有
个集合的并集共计有![]() 个.
个.
把集合![]() 中120个元素与
中120个元素与![]() 的3个元素的并集
的3个元素的并集![]()
建立一一对应关系,所以集合![]() 中元素的个数大于等于120.
中元素的个数大于等于120.
下面我们构造一个有120个元素的集合![]() :
:
把与![]() (
(![]() )对应的元素放在异于
)对应的元素放在异于![]() 的集合中,因此对于任意一个
的集合中,因此对于任意一个![]() 个集合的并集,它们都不含与
个集合的并集,它们都不含与![]() 对应的元素,所以
对应的元素,所以![]() .同时对于任意的
.同时对于任意的![]() 个集合不妨为
个集合不妨为![]() 的并集,
的并集,
则由上面的原则与![]() 对应的元素在集合
对应的元素在集合![]() 中,
中,
即对于任意的![]() 个集合
个集合![]() 的并集为全集
的并集为全集![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价﹣成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x+
(x+ ![]() ),g(x)=
),g(x)= ![]() (x﹣
(x﹣ ![]() ).
).
(1)求函数h(x)=f(x)+2g(x)的零点;
(2)求函数F(x)=[f(x)]2n﹣[g(x)]2n(n∈N*)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校游园活动有这样一个游戏:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除了颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率.
②获奖的概率.
(2)求在3次游戏中获奖次数X的分布列.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点坐标分别为A(﹣1,1),B(7,﹣1),C(﹣2,5),AB边上的中线所在直线为l.
(1)求直线l的方程;
(2)若点A关于直线l的对称点为D,求△BCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某钢管生产车间生产一批钢管,质检员从中抽出若干根对其直径(单位:![]() )进行测量,得出这批钢管的直径
)进行测量,得出这批钢管的直径![]() 服从正态分布
服从正态分布![]() .
.
(Ⅰ)如果钢管的直径![]() 满足
满足![]() 为合格品,求该批钢管为合格品的概率(精确到0.01);
为合格品,求该批钢管为合格品的概率(精确到0.01);
(Ⅱ)根据(Ⅰ)的结论,现要从40根该种钢管中任意挑选3根,求次品数![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:若![]() ,则
,则![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P,Q分别是BC和CD的中点. 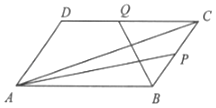
(1)若AB=2,AD=1,∠BAD=60°,求 ![]() 及cos∠BAC的余弦值;
及cos∠BAC的余弦值;
(2)若 ![]() =λ
=λ ![]() +
+ ![]() ,求λ+μ的值.
,求λ+μ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com