
【题目】如图,在三棱柱![]() 中,
中,![]() ,顶点
,顶点![]() 在底面
在底面![]() 上的射影恰为点
上的射影恰为点![]() ,且
,且![]()

(1)证明:平面![]()
![]() 平面
平面![]() ;
;
(2)求棱![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(3)若点![]() 为
为![]() 的中点,并求出二面角
的中点,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】去年年底,某商业集团公司根据相关评分细则,对其所属25家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组,其频率分布直方图如下图所示,集团公司依据评估得分,将这些连锁店划分为A,B,C,D四个等级,等级评定标准如下表所示.
评估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
评定等级 | D | C | B | A |

(1)估计该商业集团各连锁店评估得分的众数和平均数;
(2)从评估分数不小于80分的连锁店中任选2家介绍营销经验,求至少选一家A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为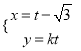 (
(![]() 为参数),直线
为参数),直线![]() 的参数程为
的参数程为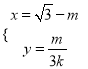 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 的动点,求点
的动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,且过点A (2,2),椭圆
的焦点为F,且过点A (2,2),椭圆![]() 的离心率为
的离心率为![]() ,点B为抛物线C与椭圆D的一个公共点,且
,点B为抛物线C与椭圆D的一个公共点,且![]() .
.
(Ⅰ)求椭圆D的方程;
(Ⅱ)过椭圆内一点P(0,t)的直线l的斜率为k,且与椭圆C交于M,N两点,设直线OM,ON(O为坐标原点)的斜率分别为k1,k2,若对任意k,存在实数λ,使得k1+ k2=λk,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,
是圆上一动点, ![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一工厂生产了某种产品700件,该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测,现将700件产品按001,002,…,700进行编号;
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;
(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100件产品的安全性能和环保性能的质量检测结果如下表:
检测结果分为优等、合格、不合格三个等级,横向和纵向分别表示安全性能和环保性能。若在该样本中,产品环保性能是优等的概率为![]() ,求
,求![]() ,
,![]() 的值。
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
(3)已知![]() ,
,![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com