
在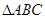 中,角
中,角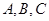 的对边分别为
的对边分别为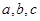 ,且
,且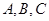 成等差数列
成等差数列
(1)若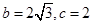 ,求
,求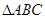 的面积
的面积
(2)若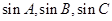 成等比数列,试判断
成等比数列,试判断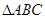 的形状
的形状
(1)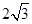 (2)等边三角形.
(2)等边三角形.
解析试题分析:(1)根据A、B、C成等差数列,结合A+B+C=π算出B= ,再由正弦定理得:
,再由正弦定理得: .根据b>c得C为锐角,得到C=
.根据b>c得C为锐角,得到C=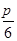 ,从而A=π-B-C=
,从而A=π-B-C=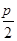 ,△ABC是直角三角形,由此不难求出它的面积.
,△ABC是直角三角形,由此不难求出它的面积.
(2)根据正弦定理,结合题意得b2=ac,根据B= ,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.
,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.
试题解析:∵A、B、C成等差数列,可得2B=A+C.
∴结合A+B+C=π,可得B= .
.
(1)∵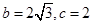 ,
,
∴由正弦定理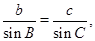 得
得 ,
,
∵b>c,可得B>C,∴C为锐角,得C=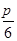 ,从而A=π-B-C=
,从而A=π-B-C=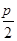 .
.
因此,△ABC的面积为S= bc=
bc= ×
×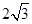 ×2=
×2=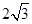 .
.
(2)∵sinA、sinB、sinC成等比数列,即sin2B=sinAsinC.
∴由正弦定理,得b2=ac
又∵根据余弦定理,得b2=a2+c2-2accosB=a2+c2-ac,
∴a2+c2-ac=ac,整理得(a-c)2=0,可得a=c
∵B= ,∴A=C=
,∴A=C= ,可得△ABC为等边三角形.
,可得△ABC为等边三角形.
考点:三角形内角和定理;利用正、余弦定理;三角形的形状判断,等差等比数列的性质.


科目:高中数学 来源: 题型:解答题
已知公差不为0的等差数列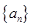 满足
满足 ,
,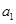 ,
,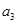 ,
,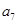 成等比数列.
成等比数列.
(1)求数列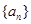 的通项公式;(2)数列
的通项公式;(2)数列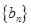 满足
满足 ,求数列
,求数列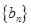 的前
的前 项和
项和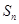 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列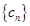 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知实数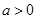 ,且
,且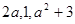 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列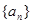 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列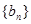 的首项和公比都为
的首项和公比都为 ,数列
,数列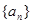 和
和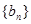 的前
的前 项和分别为
项和分别为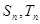 ,且
,且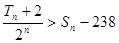 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
打一口深20米的井,打到第一米深处时需要40分钟,从第一米深处打到第二米深处需要50分钟,以后每深一米都要比前一米多10分钟,则打到最后一米深处要用 小时,打完这口井总共用 小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com