
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,且
上恒成立,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() . (2)
. (2)![]()
【解析】
(1)对函数![]() 进行求导,利用导数判断函数
进行求导,利用导数判断函数![]() 的单调性即可;
的单调性即可;
(2)令![]() ,由
,由![]() ,可得
,可得![]() ,利用分析法和放缩法的思想,通过构造函数,利用导数判断函数的单调性求最值证得当
,利用分析法和放缩法的思想,通过构造函数,利用导数判断函数的单调性求最值证得当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() 即可.
即可.
(1)依题意,![]() ,
,![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,
,
单调递减区间为![]() ,
,
(2)令![]() ,
,
由题意得,当![]() 时,
时,![]() ,则有
,则有![]() ,
,
下面证当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() ,
,
由于![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() ,
,
故只需证明对任意![]() ,都有
,都有![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,
,
所以对任意![]() ,都有
,都有![]() .
.
所以当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表. 请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期与患者年龄有关;
的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) |
| ||
50岁以下 | 55 | ||
总计 | 200 |
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立. 为了深入研究,该研究团队随机调查了![]() 名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的右焦点
的右焦点![]() 作直线
作直线![]() ,且直线
,且直线![]() 与双曲线
与双曲线![]() 的一条渐近线垂直,垂足为
的一条渐近线垂直,垂足为![]() ,直线
,直线![]() 与另一条渐近线交于点
与另一条渐近线交于点![]() ,已知
,已知![]() 为坐标原点,若
为坐标原点,若![]() 的内切圆的半径为
的内切圆的半径为![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或2
或2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的方程;
(2)已知![]() ,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
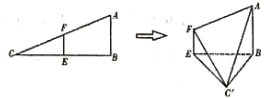
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,沿中位线DE折起后,点A对应的位置为点P,
,沿中位线DE折起后,点A对应的位置为点P,![]() .
.
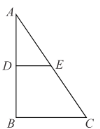
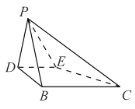
(1)求证:平面![]() 平面DBCE;
平面DBCE;
(2)求证:平面![]() 平面PCE;
平面PCE;
(3)求直线BP与平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com