
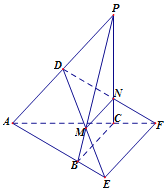
【题目】如图,在三棱锥![]() 中,
中, ![]() 两两垂直且相等,过
两两垂直且相等,过![]() 的中点
的中点![]() 作平面
作平面![]() ∥
∥![]() ,且
,且![]() 分别交PB,PC于M、N,交
分别交PB,PC于M、N,交![]() 的延长线于
的延长线于![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)运用线面垂直的判定和性质定理,以及线面平行的性质定理,即可得证;
(Ⅱ)以CA,CB,CP分别为x,y,z轴建立空间直角坐标系,并设BC=2,求出点A,B,P,D,E,F的坐标,设平面PAB的法向量和平面DEF的法向量,由向量垂直的条件:数量积为0,即可得到法向量,再由向量的夹角公式,即可得到所求二面角的余弦值.
解析:
(1)证明:由BC⊥PC,BC⊥AC可知:BC⊥平面PAC,
又因为平面α∥BC,平面AEF过BC且与平面α交于EF,
所以EF∥BC.故EF⊥平面PAC;
(2)以CA,CB,CP分别为x,y,z轴建立空间直角坐标系,
并设BC=2.则A(2,0,0),B(0,2,0),P(0,0,2),
设平面PAB的法向量![]() ,
, ![]()
D(1,0,1),E(﹣1,3,0),F(﹣1,0,0),
设平面DEF的法向量![]() ,
,
![]()
![]()
二面角P﹣DM﹣N的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 是函数
是函数![]() 的导函数,则
的导函数,则![]() 的图象大致是( )
的图象大致是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/8f50d3dfba9b485fac00e42a95909498.png] B. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/74ae44978a70424c961e850ed79072da.png]
C. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/2f113f7ec5294ba0bbd1f66b13f3e152.png] D. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/dbaa9025ccdb497380b769e5396c4c19.png]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与定直线
且与定直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,设
,设![]() 的中点为
的中点为![]() (其中
(其中![]() 为坐标原点).求证:直线
为坐标原点).求证:直线![]() 的斜率为0.
的斜率为0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为![]() .
.
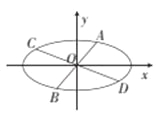
(1)若一条直径的斜率为![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为![]() 和
和![]() ,它们的斜率分别为
,它们的斜率分别为![]() ,证明:四边形
,证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
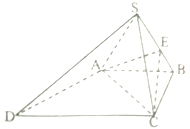
求证:(1)平面![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com