
【题目】设函数![]() ,已知方程
,已知方程![]() (
(![]() 为常数)在
为常数)在![]() 上恰有三个根,分别为
上恰有三个根,分别为![]() ,下述四个结论:
,下述四个结论:
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上恰有2个极小值点和1个极大值点;
上恰有2个极小值点和1个极大值点;
③当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,且
,且![]()
其中正确的结论个数为( )
A.1B.2C.3D.4
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一场比赛,该比赛采用三局两胜制,即先获得两局胜利者获得该场比赛胜利.在每一局比赛中,都不会出现平局,甲获胜的概率都为![]() .
.
(1)求甲在第一局失利的情况下,反败为胜的概率;
(2)若![]() ,比赛结束时,设甲获胜局数为
,比赛结束时,设甲获胜局数为![]() ,求其分布列和期望
,求其分布列和期望![]() ;
;
(3)若甲获得该场比赛胜利的概率大于甲每局获胜的概率,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一项针对我国《义务教育数学课程标准》的研究,表1为各个学段每个内容主题所包含的条目数.下图是将下表的条目数转化为百分比,按各学段绘制的等高条形图.由图表分析得出以下四个结论,其中错误的是( )
学段 内容主题 | 第一学段 (1—3年级) | 第二学段 (4—6年级) | 第三学段 (7—9年级) | 合计 |
数与代数 | 21 | 28 | 49 | 98 |
图形与几何 | 18 | 25 | 87 | 130 |
统计与概率 | 3 | 8 | 11 | 22 |
综合与实践 | 3 | 4 | 3 | 10 |
合计 | 45 | 65 | 150 | 260 |
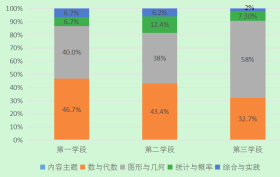
A.除了“综合与实践”外,其他三个内容领域的条目数都随着学段的升高而增加,尤其“图形与几何”在第三学段急剧增加,约是第二学段的3.5倍
B.在所有内容领域中,“图形与几何”内容最多,占![]() .“综合与实践”内容最少,约占
.“综合与实践”内容最少,约占![]()
C.第一、二学段“数与代数”内容最多,第三学段“图形与几何”内容最多
D.“数与代数”内容条目数虽然随着学段的增长而增长,而其百分比却一直在减少.“图形与几何”内容条目数,百分比都随学段的增长而增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 (
(![]() 且a为常数)和
且a为常数)和![]() (
(![]() 且k为常数),有以下命题:①当
且k为常数),有以下命题:①当![]() 时,函数
时,函数![]() 没有零点;②当
没有零点;②当![]() 时,若
时,若![]() 恰有3个不同的零点
恰有3个不同的零点![]() ,则
,则![]() ;③对任意的
;③对任意的![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 有4个不同的零点
有4个不同的零点![]() ,且
,且![]() 成等比数列.其中的真命题是_____(写出所有真命题的序号)
成等比数列.其中的真命题是_____(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
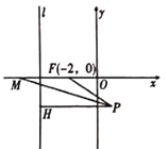
【题目】如图,在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,过动点
,过动点![]() 作
作![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交曲线
作两条直线,分别交曲线![]() 于
于![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() 的斜率之和为2时,直线
的斜率之和为2时,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
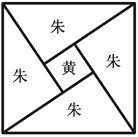
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开展学生社会法治服务项目,共设置了文明交通,社区服务,环保宣传和中国传统文化宣讲四个项目,现有该校的甲、乙、丙、丁4名学生,每名学生必须且只能选择1项.
(1)求恰有2个项目没有被这4名学生选择的概率;
(2)求“环保宣传”被这4名学生选择的人数![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com