
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(单位:分.百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
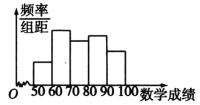
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
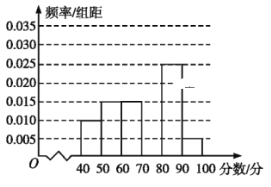
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和平均数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
【答案】(1)![]() ;作图见解析(2)众数:75;平均数:71(3)
;作图见解析(2)众数:75;平均数:71(3)![]()
【解析】
(1)由概率和为1直接计算即可求出分数在![]() 内的频率,即可直接补全频率分布直方图;
内的频率,即可直接补全频率分布直方图;
(2)直接观察频率分布直方图即可求得众数,再由平均数的计算公式即可求得平均数;
(3)由题意列出所有基本事件,找到符合要求的基本事件的个数即可得解.
(1)设分数在![]() 内的频率为
内的频率为![]() ,根据频率分布直方图,则有
,根据频率分布直方图,则有
![]() ,可得
,可得![]() .
.
则分数在![]() 内的频率为
内的频率为![]() ,频率分布直方图如下图:
,频率分布直方图如下图:
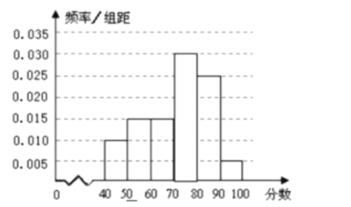
(2)由频率分布直方图可得众数为75;
平均数为![]()
![]() ,故平均数为71.
,故平均数为71.
(3)第1组:![]() 人(设为1,2,3,4,5,6),第6组:
人(设为1,2,3,4,5,6),第6组:![]() 人(设为
人(设为![]() ,
,![]() ,
,![]() ),
),
共有36个基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
满足条件的有18个,所以概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列4个说法中正确的有( )
①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() 则
则![]() ”;
”;
②若![]() ,则
,则![]() ;
;
③若复合命题:“![]() ”为假命题,则p,q均为假命题;
”为假命题,则p,q均为假命题;
④“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线上的点
,抛物线上的点![]() 到焦点的距离为2.
到焦点的距离为2.
(1)求抛物线的方程和![]() 的值;
的值;
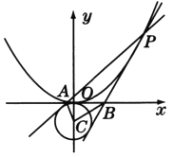
(2)如图,![]() 是抛物线上的一点,过
是抛物线上的一点,过![]() 作圆
作圆![]() 的两条切线交
的两条切线交![]() 轴于
轴于![]() ,
,![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为确定数学成绩与玩手机之间的关系,从全校随机抽样调查了40名同学,其中40%的人玩手机.这40位同学的数学分数(百分制)的茎叶图如图所示.
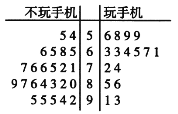
数学成绩不低于70分为良好,低于70分为一般.
(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
良好 | 一般 | 总计 | |
不玩手机 | |||
玩手机 | |||
总计 | 40 |
(2)现将40名同学的数学成绩分为如下5组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其频率分布直方图如图所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为
.其频率分布直方图如图所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),求
(同一组中的数据用该组区间的中点值作代表),求![]() 与
与![]() 的误差值.
的误差值.
(3)从这40名同学数学成绩高于90分的7人中随机选取2人介绍学习方法,求这2保不玩手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
附: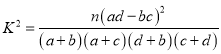 ,这40名同学的数学成绩总和为2998分.
,这40名同学的数学成绩总和为2998分.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62%B.56%
C.46%D.42%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名![]() 观众进行调查,其中有
观众进行调查,其中有![]() 名男观众和
名男观众和![]() 名女观众,将这
名女观众,将这![]() 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在
名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在![]() 分钟以上(包括
分钟以上(包括![]() 分钟)的称为“朗读爱好者”,收视时间在
分钟)的称为“朗读爱好者”,收视时间在![]() 分钟以下(不包括
分钟以下(不包括![]() 分钟)的称为“非朗读爱好者”.
分钟)的称为“非朗读爱好者”.

(1)若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取![]() 名,再从这
名,再从这![]() 名观众中任选
名观众中任选![]() 名,求至少选到
名,求至少选到![]() 名“朗读爱好者”的概率;
名“朗读爱好者”的概率;
(2)若从收视时间在40分钟以上(包括40分钟)的所有观众中选出男、女观众各1名,求选出的这两名观众时间相差5分钟以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com