Question

【题目】轮船A从某港口O要将一些物品送到正航行的轮船B上，在轮船A出发时，轮船B位于港口O北偏西30°且与O相距20海里的P处，并正以15海里/时的航速沿正东方向匀速行驶，假设轮船A沿直线方向以v海里/时的航速匀速行驶，经过t小时与轮船B相遇，

（1）若使相遇时轮船A航距最短，则轮船A的航行速度的大小应为多少？

（2）假设轮船B的航行速度为30海里/时，轮船A的最高航速只能达到30海里/时，则轮船A以多大速度及沿什么航行方向行驶才能在最短时间内与轮船B相遇，并说明理由.

Answer 1

【答案】(1) 海里/时(2) 航向为北偏东30°，航速为30海里/时时，轮船A能在最短时间内与轮船B相遇,理由见解析

【解析】

（1）设相遇时轮船A航行的距离为s海里,利用余弦定理可得,进而求得距离的最小值,从而得到此时的航行速度；

（2）先画出示意图,再利用余弦定理整理可得速度与时间的关系,根据速度的范围解得时间的最值,则可判断示意图中三角形的性质,进而得到方向即可

（1）设相遇时轮船A航行的距离为s海里，则

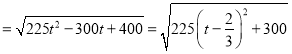
∴当时,,此时,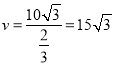

即轮船A以海里/时的速度航行,相遇时轮船A航距最短

（2）航向为北偏东30°,航速为30海里/时时,轮船A能在最短时间内与轮船B相遇,

设轮船A与轮船B在Q处相遇,如图,

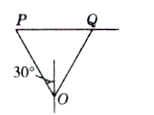
则,即,

∵,∴,即,解得,

又时,,

∴时,t最小且为,

此时在△POQ中,

∴航向为北偏东30°,航速为30海里/时时,轮船A能在最短时间内与轮船B相遇