Question

【题目】已知函数是偶函数．

（1）求k的值；

（2）若方程有实数根，求b的取值范围；

（3）设，若函数与的图象有且只有一个公共点，求实数a的取值范围．

Answer 1

【答案】（1）（2）（3）

【解析】

（1）根据函数的奇偶性得， 代入函数的解析式中，利用对数的运算法则得到 ；（2）将函数代入方程，将方程转化为两个函数交点的问题；通过判断函数 的单调性，得到其最小值，从而求得b的取值范围为 ；（3）由题意，两个函数图像有且只有一个公共点即方程有且只有一个实数根；通过讨论方程根的情况来求得参数的取值范围.

（1）∵为偶函数，∴，有，

∴对恒成立．

∴对恒成立，

∴

对恒成立，∴．

（2）由题意知，有实数根，即有解．

令，则函数的图象与直线有交点，

．

∵，∴，

∴b的取值范围是．

（3）由（1）知，，

∴由题意知有且只有一个实数根．

令，则，则关于t的方程（*）有且只有一个正根．

若，则，不合题意，舍去；

若，则方程（*）的两根异号或方程有两相等正根．

方程（*）有两相等正根等价于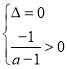，可解得．

方程（*）的两根异号等价于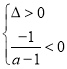，可解得．

综上所述，实数a的取值范围是．