
【题目】若定义在R上的函数![]() 满足:对于任意实数x、y,总有
满足:对于任意实数x、y,总有![]() 恒成立,我们称
恒成立,我们称![]() 为“类余弦型”函数.
为“类余弦型”函数.
![]() 已知
已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
![]() 在
在![]() 的条件下,定义数列
的条件下,定义数列![]() 2,3,
2,3,![]() 求
求![]() 的值.
的值.
![]() 若
若![]() 为“类余弦型”函数,且对于任意非零实数t,总有
为“类余弦型”函数,且对于任意非零实数t,总有![]() ,证明:函数
,证明:函数![]() 为偶函数,设有理数
为偶函数,设有理数![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)证明见解析,
(3)证明见解析,![]() ,证明见解析
,证明见解析
【解析】
![]() 是抽象函数基础题,令
是抽象函数基础题,令![]() ,求得
,求得![]() ;令
;令![]() ,求得
,求得![]() ;
;
![]() 对于此数列,需要求其通项,而求通项又需要递推公式,令
对于此数列,需要求其通项,而求通项又需要递推公式,令![]() ,
,![]() ,利用题中关系式推导出递推公式
,利用题中关系式推导出递推公式![]() ,求通项然后利用对数的运算法则求解答案;
,求通项然后利用对数的运算法则求解答案;
![]() 属于难题,因为
属于难题,因为![]() 的铺垫,代入特定的数即令
的铺垫,代入特定的数即令![]() ,y为任意实数即可证明偶函数,证明
,y为任意实数即可证明偶函数,证明![]() 与
与![]() 的大小关系需要定义新的数列,又因为题目中的有理数条件,要充分利用分数的特点.
的大小关系需要定义新的数列,又因为题目中的有理数条件,要充分利用分数的特点.
解:![]() 令
令![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() .
.
令![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() .
.
![]() 令
令![]() ,
,![]() ,其中n是大于1的整数,则
,其中n是大于1的整数,则![]() ,所以
,所以![]() ,即
,即![]() .
.
又因为![]() ,所以数列
,所以数列![]() 是首项为3,公比为2的等比数列,所以
是首项为3,公比为2的等比数列,所以![]() ,则
,则![]() .
.
所以原式![]() .
.
(3)证明:由题意函数![]() 定义域为R关于原点对称,
定义域为R关于原点对称,
令![]() ,y为任意实数,则
,y为任意实数,则![]() ,即
,即![]() ,所以
,所以![]() 是偶函数.
是偶函数.
令N为![]() ,
,![]() 分母的最小公倍数,并且
分母的最小公倍数,并且![]() ,
,![]() ,
,![]() 都是自然数,并且
都是自然数,并且![]() .
.
令数列![]() 满足
满足![]() ,
,![]() ,1,
,1,![]() 下证:数列
下证:数列![]() 单调递增.
单调递增.
![]() ,所以
,所以![]() ;
;
![]() 若
若![]() ,n是正整数,即
,n是正整数,即![]() ;
;
令![]() ,
,![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() .
.
综上,数列![]() 单调递增,所以
单调递增,所以![]() ,又因为
,又因为![]() 是偶函数,所以
是偶函数,所以![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() ,
,![]() 与
与![]() 关于抛物线的对称轴对称,斜率为1的直线交抛物线于
关于抛物线的对称轴对称,斜率为1的直线交抛物线于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 在直线
在直线![]() 两侧.
两侧.
(1)求证:![]() 平分
平分![]() ;
;
(2)点![]() 为抛物线在
为抛物线在![]() 、
、![]() 处切线的交点,若
处切线的交点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为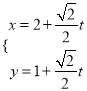 (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼乐园工作,某单位设计了统计人数的数学模型![]() ,以
,以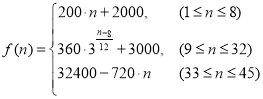 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以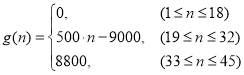 表示第
表示第![]() 个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即
个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即![]() ;9点30分作为第2个计算单位,即
;9点30分作为第2个计算单位,即![]() ;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天14点至15点这1小时内进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]()
![]() 各为多少?
各为多少?
(2)从13点45分(即![]() )开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
)开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com