
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
【答案】(1)![]() ;(2)
;(2)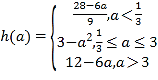 ;(3)
;(3)![]() ,
,![]()
【解析】
(1)因为![]() 的定义域为
的定义域为![]() ,所以
,所以![]() 对任意实数
对任意实数![]() 恒成立.当m=0时显然不满足,当m不为0时,内层函数为二次函数,需要开口向上且判别式小于0,即可满足要求.
恒成立.当m=0时显然不满足,当m不为0时,内层函数为二次函数,需要开口向上且判别式小于0,即可满足要求.
(2)x∈[-1,1]时,求函数![]() 是一个复合函数,复合函数的最值一般分两步来求,第一步求内层函数的值域,第二步研究外层函数在内层函数值域上的最值,本题内层函数的值域是确定的一个集合,而外层函数是一个系数有变量的二次函数,故本题是一个区间定轴动的问题.
是一个复合函数,复合函数的最值一般分两步来求,第一步求内层函数的值域,第二步研究外层函数在内层函数值域上的最值,本题内层函数的值域是确定的一个集合,而外层函数是一个系数有变量的二次函数,故本题是一个区间定轴动的问题.
(3) 根据函数的单调性,列出方程组![]() 转化为:即m、n是方程
转化为:即m、n是方程![]() 的两非负实根,且m<n.即可得解.
的两非负实根,且m<n.即可得解.
(1)由题意![]() 对任意实数
对任意实数![]() 恒成立,
恒成立,
∵![]() 时显然不满足
时显然不满足
∴![]()
∴![]()
(2)令![]() ,则
,则![]()
∴ 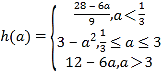
(3)∵ ![]()
∴ ![]() ∴
∴ ![]()
∴ 函数![]() 在[
在[![]() ,
,![]() ]单调递增,
]单调递增,
∴ ![]() 又∵
又∵ ![]()
∴ ![]() ,
,![]()


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校900名学生在一次百米测试中,成绩全部介于13秒与18 秒之间,利用分层抽样的方法抽取其中若干个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],有关数据见下表:
各组组员数 | 各组抽取人数 | |
[13,14) | 54 | a |
[14,15) | b | 8 |
[15,16) | 342 | 19 |
[16,17) | 288 | c |
[17,18] | d |
(1)求a,b,c,d的值;
(2)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:
(1)由△ABC中位线的性质可得![]() ,则
,则![]() 平面
平面![]() .由线面平行的判断定理可得
.由线面平行的判断定理可得![]() 平面
平面![]() .结合面面平行的判断定理可得
.结合面面平行的判断定理可得![]() 平面
平面![]() .
.
(2)由圆的性质可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,据此可知
,据此可知![]() 平面
平面![]() .利用面面垂直的判断定理可得平面
.利用面面垂直的判断定理可得平面![]() 平面
平面![]() .
.
(3)以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .结合空间几何关系计算可得平面
.结合空间几何关系计算可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() .由图可知
.由图可知![]() 为锐角,故
为锐角,故![]() .
.
试题解析:
(1)证明:因为点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)证明:因为点![]() 在以
在以![]() 为直径的
为直径的![]() 上,所以
上,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)解:如图,以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
延长![]() 交
交![]() 于点
于点![]() .因为
.因为![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() .
.
因为 ,所以
,所以![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() .
.
同理可求平面![]() 的一个法向量
的一个法向量![]() .
.
所以![]() .由图可知
.由图可知![]() 为锐角,所以
为锐角,所以![]() .
.

【题型】解答题
【结束】
21
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
(1)求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;
垂直的直线方程;
(2)在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)当x∈Z时,求A的非空真子集的个数;
(2)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数,且
是偶函数,且![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)设![]() R,求函数
R,求函数![]() 的最小值
的最小值![]() ;
;
(3)对(2)中的![]() ,若不等式
,若不等式![]() 对于任意的
对于任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com