练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）= ，其中a＞﹣1．若f（x）在R上是增函数，则实数a的取值范围是（ ）
    A.[e+1，+∞）
    B.（e+1，+∞）
    C.（e﹣1，+∞）
    D.[e﹣1，+∞）

    【答案】D
    【解析】解：∵函数f（x）= ，其中a＞﹣1在R上是增函数，
    ∴e﹣a≤ln（1+a），即ln（1+a）﹣e+a≥0，
    令g（a）=ln（1+a）﹣e+a，则g′（a）= +1，
    当a＞﹣1时，g′（a）＞0恒成立，
    又由g（e﹣1）=0，
    故ln（1+a）﹣e+a≥0可化为：a≥e﹣1，
    故实数a的取值范围是[e﹣1，+∞），
    故选：D
    【考点精析】掌握函数的最大(小)值与导数是解答本题的根本，需要知道求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

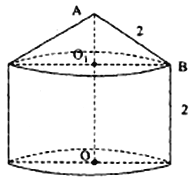
    【题目】某粮库拟建一个储粮仓如图所示，其下部是高为2的圆柱，上部是母线长为2的圆锥，现要设计其底面半径和上部圆锥的高，若设圆锥的高为，储粮仓的体积为.

    （1）求关于的函数关系式；（圆周率用表示）

    （2）求为何值时，储粮仓的体积最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和是Sn ， 且Sn+ =1．
    （1）求数列{an}的通项公式；
    （2）记bn=log3 ，数列 的前n项和为Tn ， 若不等式Tn＜m，对任意的正整数n恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知：直线，一个圆与轴正半轴与轴正半轴都相切，且圆心到直线的距离为．

    （）求圆的方程．

    （）是直线上的动点， ， 是圆的两条切线， ， 分别为切点，求四边形的面积的最小值．

    （）圆与轴交点记作，过作一直线与圆交于， 两点， 中点为，求最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4﹣5：不等式选讲
    已知函数f（x）=|x+1|﹣|x|+a．
    （1）若a=0，求不等式f（x）≥0的解集；
    （2）若方程f（x）=x有三个不同的解，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的所有零点的积为m，则有（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC=15°，沿山坡前进50m到达B处，又测得∠DBC=45°，根据以上数据可得cosθ= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a∈R，f（x）=log2（1+ax）．

    （1）求f（x2）的值域；

    （2）若关于x的方程f（x）-log2[（a-4）x2+（2a-5）x]=0的解集恰有一个元素，求实数a的取值范围；

    （3）当a＞0时，对任意的t∈（，+∞），f（x2）在[t，t+1]的最大值与最小值的差不超过4，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4﹣1：几何证明选讲
    如图，已知四边形ABCD内接于⊙O，且AB是的⊙O直径，过点D的⊙O的切线与BA的延长线交于点M．

    （1）若MD=6，MB=12，求AB的长；
    （2）若AM=AD，求∠DCB的大小．

    查看答案和解析>>

    同步练习册答案