
【题目】设函数![]() x∈R,其中a,b∈R.
x∈R,其中a,b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0,且f(x1)= f(x0),其中x1≠x0,求证:x1+2x0=3;
(Ⅲ)设a>0,函数g(x)= |f(x)|,求证:g(x)在区间[0,2]上的最大值不小于![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
试题(Ⅰ)先求函数的导数![]() ,再根据导函数零点是否存在,分类讨论;(Ⅱ)由题意得
,再根据导函数零点是否存在,分类讨论;(Ⅱ)由题意得![]() ,计算可得
,计算可得![]() .再由
.再由![]() 及单调性可得结论;(Ⅲ)实质研究函数
及单调性可得结论;(Ⅲ)实质研究函数![]() 最大值:主要比较
最大值:主要比较![]() ,
,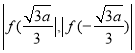 的大小即可,可分三种情况研究:①
的大小即可,可分三种情况研究:①![]() ;②
;②![]() ;③
;③![]() .
.
试题解析:(Ⅰ)解:由![]() ,可得
,可得![]() .
.
下面分两种情况讨论:
(1)当![]() 时,有
时,有![]() 恒成立,所以
恒成立,所以![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)当![]() 时,令
时,令![]() ,解得
,解得![]() ,或
,或![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() .
.
(Ⅱ)证明:因为![]() 存在极值点,所以由(Ⅰ)知
存在极值点,所以由(Ⅰ)知![]() ,且
,且![]() ,
,
由题意,得![]() ,即
,即![]() ,
,
进而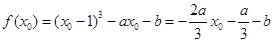 .
.
又![]()
![]() ,且
,且![]() ,由题意及(Ⅰ)知,存在唯一实数
,由题意及(Ⅰ)知,存在唯一实数![]() 满足
满足![]() ,且
,且![]() ,因此
,因此![]() ,所以
,所以![]() .
.
(Ⅲ)证明:设![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,![]() 表示
表示![]() 两数的最大值.下面分三种情况讨论:
两数的最大值.下面分三种情况讨论:
(1)当![]() 时,
时,![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() 在区间
在区间![]() 上单调递减,所以
上单调递减,所以![]() 在区间
在区间![]() 上的取值范围为
上的取值范围为![]() ,因此
,因此
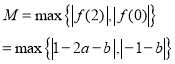
![]()
![]() ,
,
所以![]() .
.
(2)当![]() 时,
时,![]() ,由(Ⅰ)和(Ⅱ)知,
,由(Ⅰ)和(Ⅱ)知,![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 上的取值范围为
上的取值范围为![]() ,因此
,因此
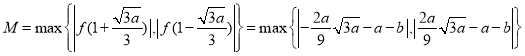
![]()
![]() .
.
(3)当![]() 时,
时,![]() ,由(Ⅰ)和(Ⅱ)知,
,由(Ⅰ)和(Ⅱ)知,
![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 上的取值范围为
上的取值范围为![]() ,因此
,因此
![]()
![]()
![]() .
.
综上所述,当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() .
.


科目:高中数学 来源: 题型:
【题目】我国唐代天文学家、数学家张逐曾以“李白喝酒”为题编写了如下一道题:“李白街上走,提壶去买酒,遇店加一倍,见花喝一斗(计量单位),三遇店和花,喝光壶中酒.”问最后一次遇花时有酒________斗,原有酒________斗.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过抛物线的焦点
,过抛物线的焦点![]() 且与
且与![]() 轴垂直的直线与抛物线在第一象限交于点
轴垂直的直线与抛物线在第一象限交于点![]() ,
,![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求抛物线的标准方程;
(2)若![]() ,
,![]() ,
,![]() 为抛物线上的两个不同的点,直线
为抛物线上的两个不同的点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]()
![]() ,求点
,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进人市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进人市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如表所示:
表1
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示).
(2)试问甲、乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
(3)若以甲公司这100天中每天产品利润总和对应的频率作为概率,从甲公司这100天随机抽取1天,记这天产品利润总和为X,求X的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() 若数列
若数列![]() 满足
满足![]() 其中
其中![]() 则称
则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(I)数列![]() 是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(II)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(III)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() 且
且![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海举办,本届展会共有来自172个国家、地区和国际组织参会,3600多家企业参展,超过40万名采购商到会洽谈采购,其中中国馆更是吸引众人眼球.为了使博览会有序进行,组委会安排6名志愿者到中国馆的某4个展区提供服务,要求![]() 展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
展区各安排一名志愿者,其余两个展区各安排两名志愿者,其中小马和小王不在一起,则不同的安排方案共有( )
A.156种B.168种C.172种D.180种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com