
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 上的值域;
上的值域;
(2)试求![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
【答案】(1)![]() (2)当
(2)当![]() 时,
时, ![]() 只有一个零点;当
只有一个零点;当![]() 时,
时, ![]() 有两个零点.
有两个零点.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,而
,而![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上递减,由
上递减,由![]() ,可得
,可得
当![]() 时,
时, ![]() ,
, ![]() 递增;当
递增;当![]() 时
时![]() ,
, ![]() 递减;所以
递减;所以![]() ,比较
,比较![]() 的大小可得
的大小可得![]() ,进而可得结果;
,进而可得结果;
(2)原方程等价于![]() 实根的个数,原命题也等价于
实根的个数,原命题也等价于![]() 在
在![]() 上的零点个数,讨论
上的零点个数,讨论![]() ,
, ![]() ,
, ![]() ,三种情况,分别利用导数研究函数的单调性,结合函数图象与零点存在定理可得结果.
,三种情况,分别利用导数研究函数的单调性,结合函数图象与零点存在定理可得结果.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,
,
而![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上递减,
上递减,
![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上存在唯一的
上存在唯一的![]() ,使得
,使得![]() ,而且
,而且
当![]() 时,
时, ![]() ,
, ![]() 递增;当
递增;当![]() 时
时![]() ,
, ![]() 递减;
递减;
所以,当![]() 时,
时, ![]() 取极大值,也是最大值,即
取极大值,也是最大值,即![]() ,
,
![]() ,
,
所以, ![]() 在
在![]() 上的值域为
上的值域为![]() .
.
(2)令![]() ,得
,得![]() ,
, ![]() 显然不是方程的根,
显然不是方程的根,
那么原方程等价于![]() 实根的个数,令
实根的个数,令![]() ,
, ![]()
原命题也等价于![]() 在
在![]() 上的零点个数;
上的零点个数;
又因为![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上都是单调递增的;
上都是单调递增的;
(I)若![]() ,则
,则
当![]() 时,
时, ![]() 恒成立,则没有零点;
恒成立,则没有零点;
当![]() 时,
时, ![]() ,
, ![]() ,又
,又![]() 在
在![]() 上单调递增的,所以有唯一的零点。
上单调递增的,所以有唯一的零点。
(II)若![]() ,则
,则
当![]() 时,
时, ![]() 恒成立,则没有零点;
恒成立,则没有零点;
当![]() 时,
时, ![]() ,
, ![]() ,又
,又![]() 在
在![]() 上单调递增的,所以有唯一的零点
上单调递增的,所以有唯一的零点
(III)若![]() ,则
,则
当![]() 时,由
时,由 ![]() ,则
,则![]() ,
,
则![]() 取
取![]() ,则
,则![]() ,又
,又![]() ,所以
,所以![]() 在
在![]() 有唯一的零点,
有唯一的零点,
当![]() 时,
时, ![]() ,
,
![]() ,又
,又![]() 在
在![]() 上单调递增的,所以有唯一的零点
上单调递增的,所以有唯一的零点
综上所述,当![]() 时,
时, ![]() 只有一个零点;当
只有一个零点;当![]() 时,
时, ![]() 有两个零点.
有两个零点.


科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=![]() ,an+1-
,an+1-![]() an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
(1)求实数λ;
(2)求数列{an}的通项公式;
(3)设![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用,如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输出的![]() 的值为0,则输入的
的值为0,则输入的![]() 的值为( )
的值为( )
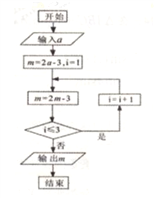
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为![]() ,则由此可估计
,则由此可估计![]() 的近似值为( )
的近似值为( )
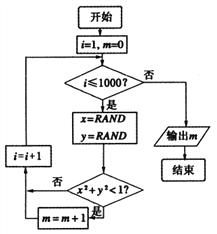
A. 3.119 B. 3.124 C. 3.132 D. 3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机将1,2,…,2n(n∈N*,n≥2)这2n个连续正整数分成A,B两组,每组n个数.A组最小数为a1,最大数为a2;B组最小数为b1,最大数为b2,记ξ=a2-a1,η=b2-b1.
(1)当n=3时,求ξ的分布列和数学期望;
(2)令C表示事件“ξ与η的取值恰好相等”,求事件C发生的概率P(C);
(3)对(2)中的事件C, ![]() 表示C的对立事件,判断P(C)和P(
表示C的对立事件,判断P(C)和P(![]() )的大小关系,并说明理由.
)的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com