练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，抛物线的焦点为，过点作直线与抛物线交于、两点，当直线与轴垂直时长为.

    （1）求抛物线的方程；

    （2）若与的面积相等，求直线的方程.

    【答案】（1）；（2）或.

    【解析】

    （1）由题意可知点在抛物线上，将该点坐标代入抛物线的方程，求得的值，进而可求得抛物线的方程；

    （2）由题意得出，可得知直线的斜率不为零，可设直线的方程为，将该直线方程与抛物线方程连理，列出韦达定理，由题意得出，代入韦达定理后可求得的值，进而可求得直线的方程.

    （1）当直线与轴垂直时的长为，

    又，取，所以，解得，

    所以抛物线的方程为；

    （2）由题意知，，

    因，所以，

    当时，直线与抛物线不存在两个交点，所以，

    故设直线的方程为，代入抛物线方程得，

    所以，，，

    可得，解得.

    所以，直线的方程为或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某班级有60名学生，学号分别为1～60，其中男生35人，女生25人．为了了解学生的体质情况，甲、乙两人对全班最近一次体育测试的成绩分别进行了随机抽样．其中一人用的是系统抽样，另一人用的是分层抽样，他们得到各12人的样本数据如下所示，并规定体育成绩大于或等于80人为优秀．

    甲抽取的样本数据：

    学号

    4

    9

    14

    19

    24

    29

    34

    39

    44

    49

    54

    59

    性别

    男

    女

    男

    男

    女

    男

    女

    男

    女

    女

    男

    男

    体育成绩

    90

    80

    75

    80

    83

    85

    75

    80

    70

    80

    83

    70

    女抽取的样本数据：

    学号

    1

    8

    10

    20

    23

    28

    33

    35

    43

    48

    52

    57

    性别

    男

    男

    男

    男

    男

    男

    男

    女

    女

    女

    女

    女

    体育成绩

    95

    85

    85

    80

    70

    80

    80

    65

    70

    60

    70

    80

    （Ⅰ）在乙抽取的样本中任取4人，记这4人中体育成绩优秀的学生人数为，求的分布列和数学期望；

    （Ⅱ）请你根据乙抽取的样本数据，判断是否有95%的把握认为体育成绩是否为优秀和性别有关；

    （Ⅲ）判断甲、乙各用的何种抽样方法，并根据（Ⅱ）的结论判断哪种抽样方法更优，说明理由．

    附：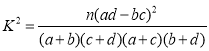

    0.15

    0.10

    0.05

    0.010

    0.005

    0.001

    k

    2.072

    2.706

    3.841

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正四棱锥的侧棱和底面边长相等，在这个正四棱锥的条棱中任取两条，按下列方式定义随机变量的值：

    若这两条棱所在的直线相交，则的值是这两条棱所在直线的夹角大小（弧度制）；

    若这两条棱所在的直线平行，则；

    若这两条棱所在的直线异面，则的值是这两条棱所在直线所成角的大小(弧度制).

    （1）求的值；

    （2）求随机变量的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥中，与均为等腰直角三角形，且，，为上一点，且平面.

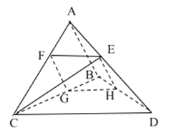
    （1）求证：；

    （2）过作一平面分别交， ， 于，，，若四边形为平行四边形，求多面体的表面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P—ABCD中，底面ABCD是菱形，PC⊥BC，点E是PC的中点，且平面PBC⊥平面ABCD.求证：

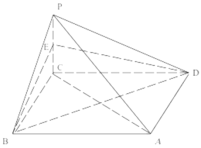
    （1）求证：PA∥平面BDE；

    （2）求证：平面PAC⊥平面BDE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中某班共有40个学生，将学生的身高分成4组：平频率/组距，，，进行统计，作成如图所示的频率分布直方图．

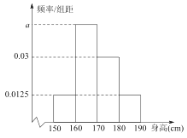
    （1）求频率分布直方图中的值和身高在内的人数；

    （2）求这40个学生平均身高的估计值（同一组中的数据用该组区间的中点值为代表）（精确到0.01）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

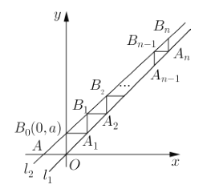
    【题目】已知直线，斜率为的直线与x轴交于点A，与y轴交于点，过作x 轴的平行线，交于点，过作y轴的平行线，交于点，再过作x轴的平行线交于点，…，这样依次得线段、、、、…、、，记为点的横坐标，则__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是椭圆C： 上一点，点P到椭圆C的两个焦点的距离之和为.

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线交于点M，

    是否存在点A，使得？若存在，求出点A的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求函数的单调区间；

    （2）己知函数有两个极值点

    ①比较与的大小；

    ②若函数在区间上有且只有一个零点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案