练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某高中某班共有40个学生，将学生的身高分成4组：平频率/组距，，，进行统计，作成如图所示的频率分布直方图．

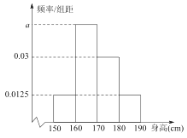
    （1）求频率分布直方图中的值和身高在内的人数；

    （2）求这40个学生平均身高的估计值（同一组中的数据用该组区间的中点值为代表）（精确到0.01）．

    【答案】（1）0.0450；18人，（2）．

    【解析】

    （1）根据频率分布直方图和频率的定义可得的值，计算身高在内的频率，由此能估计身高在内的人数；

    （2）同一组中的数据用该组区间的中点值为代表，直接计算可得平均身高的估计值.

    （1）由图可得，，三组的频率分别为0.1250，0.3000，0.1250

    所以

    所以身高在内的人数为：（人）

    （2）这40个学生平均身高的估计值为

    所以这40个学生平均身高的估计值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.（为自然对数的底数）

    （1）当时，设，求函数在上的最值；

    （2）当时，证明：，其中（表示中较小的数.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn,且Sn＝n（n+2）（n∈N*）.

    （1）求数列{an}的通项公式；

    （2）设bn,求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数(，).

    （1）当时，若函数在上有两个零点，求的取值范围；

    （2）当时，是否存在，使得不等式恒成立？若存在，求出的取值集合；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，抛物线的焦点为，过点作直线与抛物线交于、两点，当直线与轴垂直时长为.

    （1）求抛物线的方程；

    （2）若与的面积相等，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着经济的快速增长、规模的迅速扩张以及人民生活水平的逐渐提高，日益剧增的垃圾给城市的绿色发展带来了巨大的压力.相关部门在有5万居民的光明社区采用分层抽样方法得到年内家庭人均与人均垃圾清运量的统计数据如下表：

    人均（万元/人）

    3

    6

    9

    12

    15

    人均垃圾清运量（吨/人）

    0.13

    0.23

    0.31

    0.41

    0.52

    （1）已知变量与之间存在线性相关关系，求出其回归直线方程；

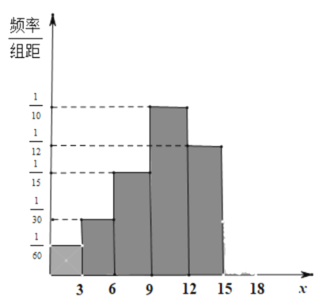
    （2）随着垃圾分类的推进，燃烧垃圾发电的热值大幅上升，平均每吨垃圾可折算成上网电量200千瓦时，如图是光明社区年内家庭人均的频率分布直方图，请补全的缺失部分，并利用（1）的结果，估计整个光明社区年内垃圾可折算成的总上网电量.

    参考公式]回归方程，

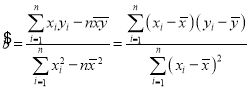
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，A、B分别为椭圆的上、下顶点，若动直线l过点，且与椭圆相交于C、D两个不同点（直线l与y轴不重合，且C、D两点在y轴右侧，C在D的上方），直线AD与BC相交于点Q．

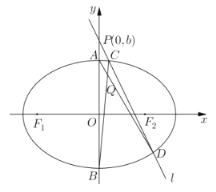
    （1）设的两焦点为、，求的值;

    （2）若，且，求点Q的横坐标；

    （3）是否存在这样的点P，使得点Q的纵坐标恒为？若存在，求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，，，直线AG，BG相交于点G，且它们的斜率之积为.记点G的轨迹为曲线C.

    （1）若射线与曲线C交于点D，且E为曲线C的最高点，证明：.

    （2）直线与曲线C交于M，N两点，直线AM，AN与y轴分别交于P，Q两点.试问在x轴上是否存在定点T，使得以PQ为直径的圆恒过点T？若存在，求出T的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了治理空气污染，某市设9个监测站用于监测空气质量指数（AQI），其中在轻度污染区、中度污染区、重度污染区分别设有2、4、3个监测站，并以9个监测站测得的AQI的平均值为依据播报该市的空气质量.

    （1）若某日播报的AQI为119，已知轻度污染区AQI平均值为70，中度污染区AQI平均值为115，求重试污染区AQI平均值；

    （2）如图是2018年11月份30天的AQI的频率分布直方图，11月份仅有1天AQI在内.

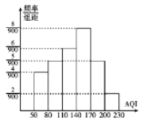
    ①某校参照官方公布的AQI，如果周日AQI小于150就组织学生参加户外活动，以统计数据中的频率为概率，求该校学生周日能参加户外活动的概率；

    ②环卫部门从11月份AQI不小于170的数据中抽取三天的数据进行研究，求抽取的这三天中AQI值不小于200的天数的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案