
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)己知函数![]() 有两个极值点
有两个极值点![]()
①比较![]() 与
与![]() 的大小;
的大小;
②若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,具体见解析;(2)①![]() ;②
;②![]()
【解析】
(1)![]() ,分
,分![]() ,
,![]() 两种情况讨论即可;
两种情况讨论即可;
(2)①通过因式分解可得![]() 的表达式,再利用
的表达式,再利用![]() 是函数
是函数![]() 有两个极值点
有两个极值点![]() 得到
得到![]() ,
,![]() ,代入计算即可得到
,代入计算即可得到![]() 与
与![]() 的大小;②由题意可将问题转化为
的大小;②由题意可将问题转化为![]() 在区间
在区间![]() 上有唯一的最大值
上有唯一的最大值![]() ,进一步可得到
,进一步可得到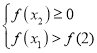 或
或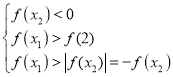 ,结合
,结合![]() ,分别解不等式组即可.
,分别解不等式组即可.
(1)![]() .
.
当![]() 时,
时,![]() ,
,
所以![]() 的单调增区间为
的单调增区间为![]() ,无减区间;
,无减区间;
当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
令![]() ,得
,得![]()
![]() ,
,
所以![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,
,
减区间为![]() .
.
综上:当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() 无减区间
无减区间
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,
,
减区间为![]() .
.
(2)因为![]() 的两个极值点
的两个极值点![]() ,
,![]() ,
,
由(1)知,当![]() 时,
时,
![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
因此![]() ,
,
所以![]() .
.
①因为![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上递减,
上递减,
所以![]() ,
,![]() .
.
由![]()
![]()
![]()
![]()
即![]() .
.
②因为函数![]() 在区间
在区间![]() 上有且只有一个零点,
上有且只有一个零点,
所以![]() 在区间
在区间![]() 上只有唯一的最大值
上只有唯一的最大值![]() .
.
故由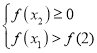 (由①知不成立,故舍去)
(由①知不成立,故舍去)
或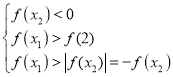 (即
(即![]() )
)
由![]() ,
,
解得![]() ,代入
,代入![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,极点为![]() ,一条封闭的曲线
,一条封闭的曲线![]() 由四段曲线组成:
由四段曲线组成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该封闭曲线所围成的图形面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 恰有3个公共点,求
恰有3个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为平面上一点,
为平面上一点,![]() 为直线
为直线![]() :
:![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,设线段
,设线段![]() 的中垂线与直线
的中垂线与直线![]() 交于点
交于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的直线
作互相垂直的直线![]() 与
与![]() ,其中直线
,其中直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,设点
,设点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,求
的中点,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理空气污染,某市设9个监测站用于监测空气质量指数(AQI),其中在轻度污染区、中度污染区、重度污染区分别设有2、4、3个监测站,并以9个监测站测得的AQI的平均值为依据播报该市的空气质量.
(1)若某日播报的AQI为119,已知轻度污染区AQI平均值为70,中度污染区AQI平均值为115,求重试污染区AQI平均值;
(2)如图是2018年11月份30天的AQI的频率分布直方图,11月份仅有1天AQI在![]() 内.
内.
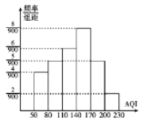
①某校参照官方公布的AQI,如果周日AQI小于150就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从11月份AQI不小于170的数据中抽取三天的数据进行研究,求抽取的这三天中AQI值不小于200的天数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的![]() ,得到“徵”;“徵”经过一次“益”,频率变为原来的
,得到“徵”;“徵”经过一次“益”,频率变为原来的![]() ,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列D.“徵、商、羽”的频率成等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com