
【题目】已知函数f(x)=sin2x+2 ![]() sin(x+
sin(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() )﹣cos2x﹣
)﹣cos2x﹣ ![]() .
.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在[﹣ ![]() ,
, ![]() π]上的最大值.
π]上的最大值.
【答案】
(1)解:∵函数f(x)=sin2x+2 ![]() sin(x+
sin(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() )﹣cos2x﹣
)﹣cos2x﹣ ![]()
=﹣cos2x+2 ![]() (
( ![]() sinx+
sinx+ ![]() cosx)(
cosx)( ![]() cosx+
cosx+ ![]() sinx)﹣
sinx)﹣ ![]() =﹣cos2x+2
=﹣cos2x+2 ![]() (
( ![]() +
+ ![]() sin2x)﹣
sin2x)﹣ ![]()
= ![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣ ![]() ),
),
令2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ+
,求得kπ+ ![]() ≤x≤kπ
≤x≤kπ ![]() ,可得函数的减区间为[kπ+
,可得函数的减区间为[kπ+ ![]() ,kπ
,kπ ![]() ],k∈Z
],k∈Z
(2)解:在[﹣ ![]() ,
, ![]() π]上,2x﹣
π]上,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故当2x﹣
],故当2x﹣ ![]() =
= ![]() 时,函数f(x)取得最大值为2
时,函数f(x)取得最大值为2
【解析】(1)利用三角恒等变换化简函数的解析式,再利用正弦函数的单调性求得函数的减区间.(2)利用正弦函数的定义域和值域,求得函数f(x)在[﹣ ![]() ,
, ![]() π]上的最大值.
π]上的最大值.
【考点精析】本题主要考查了正弦函数的单调性和三角函数的最值的相关知识点,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;函数
上是减函数;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求第3,4,5组的频率;
(2)为了了解最优秀学生的情况,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=a(a∈R),an+1= ![]() ,n∈N*;
,n∈N*;
(1)若0<an≤6,求证:0<an+1≤6;
(2)若a=5,求S2016;
(3)若a= ![]() (m∈N*),求S4m+2的值.
(m∈N*),求S4m+2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为不等于1的正数,数列{bn}满足bn=lgan,b3=18,b6=12,则数列{bn}的前n项和的最大值等于( )
A. 126 B. 130 C. 132 D. 134
【答案】C
【解析】
由题意可知,lga3=b3,lga6=b6再由b3,b6,用a1和q表示出a3和b6,进而求得q和a1,根据{an}为正项等比数列推知{bn}为等差数列,进而得出数列bn的通项公式和前n项和,可知Sn的表达式为一元二次函数,根据其单调性进而求得Sn的最大值.
由题意可知,lga3=b3,lga6=b6.
又∵b3=18,b6=12,则a1q2=1018,a1q5=1012,
∴q3=10﹣6.
即q=10﹣2,∴a1=1022.
又∵{an}为正项等比数列,
∴{bn}为等差数列,
且d=﹣2,b1=22.
故bn=22+(n﹣1)×(﹣2)=﹣2n+24.
∴Sn=22n+![]() ×(﹣2)
×(﹣2)
=﹣n2+23n=![]() ,又∵n∈N*,故n=11或12时,(Sn)max=132.
,又∵n∈N*,故n=11或12时,(Sn)max=132.
故答案为:C.
【点睛】
这个题目考查的是等比数列的性质和应用;解决等差等比数列的小题时,常见的思路是可以化基本量,解方程;利用等差等比数列的性质解决题目;还有就是如果题目中涉及到的项较多时,可以观察项和项之间的脚码间的关系,也可以通过这个发现规律。
【题型】单选题
【结束】
12
【题目】已知数列![]() 是递增数列,且对
是递增数列,且对![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列性制的函数f(x)的全体,存在实数a、k(k≠0),对于定义域内的任意x均有f(a+x)=kf(a﹣x)成立,称数对(a,k)为函数f(x)的“伴随数对”.
(1)判断f(x)=x2是否属于集合M,并说明理由;
(2)若函数f(x)=sinx∈M,求满足条件的函数f(x)的所有“伴随数对”;
(3)若(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,当1≤x<2时,f(x)=cos( ![]() x);当x=2时,f(x)=0,求当2014≤x≤2016时,函数y=f(x)的解析式和零点.
x);当x=2时,f(x)=0,求当2014≤x≤2016时,函数y=f(x)的解析式和零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是等差数列{an}的前n项和,已知![]() 与
与![]() 的等比中项为
的等比中项为![]() ,且
,且![]() 与
与![]() 的等差中项为1,求数列{an}的通项公式。
的等差中项为1,求数列{an}的通项公式。
【答案】![]() 或
或![]() .
.
【解析】
设等差数列{an}的首项为a1,公差为d,运用等差中项和等比中项的定义,利用等差数列的求和公式,代入可求a1,d,解方程可求通项an.
设等差数列{an}的首项![]() ,公差为
,公差为![]() ,则通项为
,则通项为![]() ,
,
前![]() 项和为
项和为![]() ,依题意有
,依题意有 ,
,
其中![]() ,由此可得
,由此可得 ,
,
整理得 , 解方程组得
, 解方程组得![]() 或
或 ,
,
由此得![]() ;或
;或![]() .
.
经检验![]() 和
和![]() 均合题意.
均合题意.
所以所求等差数列的通项公式为![]() 或
或![]() .
.
【点睛】
本题主要考查了等差数列的通项公式和性质及等比数列中项的性质,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用。
做差得通项,但是这种方法需要检验n=1时通项公式是否适用。
【题型】解答题
【结束】
20
【题目】等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a,b,c∈R.
,其中a,b,c∈R.
(1)若a=b=c=1,求f(x)的单调区间;
(2)若b=c=1,且当x≥0时,f(x)≥1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
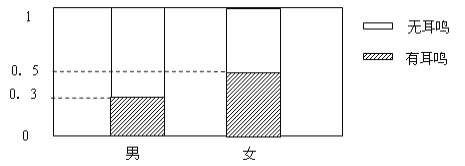
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com