
【题目】若集合![]() 满足
满足![]() ,则称
,则称![]() 为集合
为集合![]() 的一种分拆,并规定:当且仅当
的一种分拆,并规定:当且仅当![]() 时,
时, ![]() 与
与![]() 是集合
是集合![]() 的同一种分拆。若集合
的同一种分拆。若集合![]() 有三个元素,则集合
有三个元素,则集合![]() 的不同分拆种数是 .
的不同分拆种数是 .
【答案】27
【解析】
试题分析:设![]()
①若![]() =时,
=时,![]() =A,此时只有一种分拆.
=A,此时只有一种分拆.
②若![]() 是单元素集时,共有六种分拆,{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}.
是单元素集时,共有六种分拆,{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}.
③若![]() 是双元素集时,共有12种,{1,2}与{3},{1,3},{2,3},{1,2,3};
是双元素集时,共有12种,{1,2}与{3},{1,3},{2,3},{1,2,3};
{1,3}与{2},{1,2},{2,3},{1,2,3};
{2,3}与{1},{1,2},{1,3},{1,2,3};
④若![]() =A={1,2,3},则
=A={1,2,3},则![]() =,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3}共8种.
=,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3}共8种.
综上有1+6+12+8=27


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某旅行社设计了一个组织旅游团包飞机去广州旅游的方案,其中旅行杜的包机费用为![]() 元,旅游团中最多能有
元,旅游团中最多能有![]() 人,并且旅游团中的人数
人,并且旅游团中的人数![]() (单位:个)与每个人交给旅行社的费用
(单位:个)与每个人交给旅行社的费用![]() (单位:元)的关系如下:
(单位:元)的关系如下: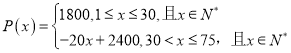 .
.
(1)将旅行社的利润![]() (单位:元)表示成旅游团中的人数
(单位:元)表示成旅游团中的人数![]() 的函数(注:利润=收取的费用一包机费用);
的函数(注:利润=收取的费用一包机费用);
(2)当旅游团有多少人时,旅行社的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(3)记集合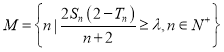 ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2![]() 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为![]() 元/
元/![]() ,新墙的造价为
,新墙的造价为![]() 元/
元/![]() ,设利用的旧墙的长度为
,设利用的旧墙的长度为![]() ,费用为
,费用为![]() 元.
元.
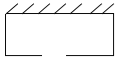
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
(Ⅰ)求f(x)定义域;
(Ⅱ)判断f(x)的奇偶性,并说明理由;
(Ⅲ)求使f(x)>0的x的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com