
【题目】设函数![]() 在
在![]() 上是奇函数,且对任意
上是奇函数,且对任意![]() 都有
都有![]() ,当
,当![]() 时,
时,![]() ,
,![]() :
:
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断![]() 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅲ)求不等式![]() 的解集.
的解集.
【答案】(Ⅰ)![]() (Ⅱ)单调递减(Ⅲ)
(Ⅱ)单调递减(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)在f(x+y)=f(x)+f(y)中,令x=y=1,即可得出;(Ⅱ)结论:函数f(x)在[-3,3]上是单调递减的,如下:任取-3≤![]() ≤3,f(
≤3,f(![]() )-f(
)-f(![]() )=f(
)=f(![]() )<0,即可判断出结论;
)<0,即可判断出结论;
(Ⅲ)由于f(2)=-4,不等式f(x-1)>4等价于f(x-1)>-f(2)=f(-2),又根据函数f(x)在[-3,3]上是单调递减,即可得出
试题解析:(Ⅰ)在![]() 中,令
中,令![]() 得
得
![]() …………………3 分
…………………3 分
(Ⅱ)结论:函数![]() 在
在![]() 上是单调递减的,证明如下:
上是单调递减的,证明如下:
任取![]()
则![]() =
=![]() =
=![]()
因为![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]()
故函数![]() 在
在![]() 上单调递减。…………………7 分
上单调递减。…………………7 分
(Ⅲ)由于![]()
所以不等式![]() 等价于
等价于![]()
又![]() 是奇函数,所以
是奇函数,所以![]()
即![]()
又因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,解得
,解得![]()
故原不等式的解集为![]() …………………12分
…………………12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
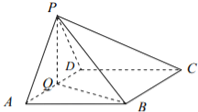
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点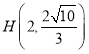 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问:![]() 的周长是否为定值?若是,求出定值;若不是。说明理由.
的周长是否为定值?若是,求出定值;若不是。说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x.
(1)求函数f(x)的极值点;
(2)设函数g(x)=f(x)-a(x-1),其中a∈R,求函数g(x)在区间[1,e]上的最小值.(其中e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有6个红球和5个白球的口袋中任取4个球,那么下列是互斥而不对立的事件是( )
A. 至少一个红球与都是红球
B. 至少一个红球与至少一个白球
C. 至少一个红球与都是白球
D. 恰有一个红球与恰有两个红球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com