
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线方程为
所在直线方程为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据条件由点斜式求出直线AC的方程,然后将直线AC,CM的方程联立得到方程组,解方程组可得点C的坐标;(2)设出点B的坐标(x0,y0),由中点坐标公式求出点M的坐标(![]() ,
, ![]() ),根据点M在CM上可得关于x0,y0的方程,又
),根据点M在CM上可得关于x0,y0的方程,又![]() ,可求得B(0,-3),最后根据两点式可得直线
,可求得B(0,-3),最后根据两点式可得直线![]() 的方程
的方程
试题解析:
(1)依题意知直线AC的斜率为![]() ,
,
∴直线AC的方程为![]() ,即2x+y-13=0,
,即2x+y-13=0,
由![]() ,解得
,解得![]()
∴点C的坐标为(5,3).
(2)设B(x0,y0),AB的中点M为(![]() ,
, ![]() ),
),
代入2x-y-7=0,得2x0-y0-3=0,
由![]() ,解得
,解得![]() ,
,
∴点B坐标为(0,-3),
∴直线BC的方程为![]() ,
,
即6x-5y-15=0.


科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
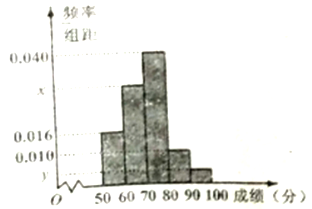

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
, ![]() 的值;
的值;
(Ⅱ)分数在![]() 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在![]() 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() 的值.
的值.
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=![]() , AD=1,DC⊥BC,则这块菜地的面积为
, AD=1,DC⊥BC,则这块菜地的面积为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com