
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)当 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;
(3)记函数 图象为曲线
图象为曲线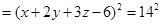 ,设点
,设点 ,
, 是曲线
是曲线 上不同的两点,点
上不同的两点,点 为线段
为线段 的中点,过点
的中点,过点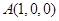 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 .试问:曲线
.试问:曲线 在点
在点 处的切线是否平行于直线
处的切线是否平行于直线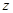 ?并说明理由.
?并说明理由.
(1) ,(2)
,(2) (3)不平行
(3)不平行
解析试题分析:(1)利用导数求函数单调区间,分四步:第一步,求定义域, ,第二步,求导,
,第二步,求导,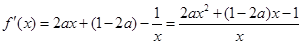 ,关键在因式分解,目的解不等式. 第三步解不等式由
,关键在因式分解,目的解不等式. 第三步解不等式由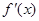
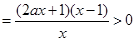 ,得
,得 ,第四步,写结论,
,第四步,写结论, 的单调增区间为
的单调增区间为 .(2)求函数最值,其实质还是研究其单调性. 当
.(2)求函数最值,其实质还是研究其单调性. 当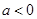 时,由
时,由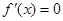 ,得
,得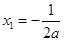 ,
,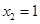 ,①当
,①当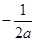 >1,即
>1,即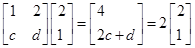 时,
时,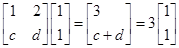 在
在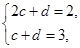 上是减函数,所以
上是减函数,所以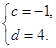 在
在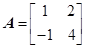 上的最小值为
上的最小值为 .②当
.②当 ,即
,即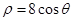 时,
时, 在
在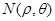 上是减函数,在
上是减函数,在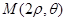 上是增函数,所以
上是增函数,所以 的最小值为
的最小值为 .③当
.③当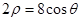 ,即
,即 时,
时, 在
在 上是增函数,所以
上是增函数,所以 的最小值为
的最小值为 .(3)是否平行,还是从假设平行出发,探究等量关系是否成立. 设
.(3)是否平行,还是从假设平行出发,探究等量关系是否成立. 设 ,则点N的横坐标为
,则点N的横坐标为 ,直线AB的斜率
,直线AB的斜率 =
= ,曲线C在点N处的切线斜率
,曲线C在点N处的切线斜率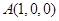

 ,由
,由 得
得 ,不妨设
,不妨设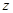 ,
,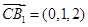 ,则
,则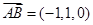 ,下面研究函数
,下面研究函数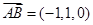 是否有大于1的解.易由函数单调性得方程无解.
是否有大于1的解.易由函数单调性得方程无解.
试题解析:(1)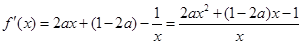
 , 2分
, 2分
因为 ,
, ,所以
,所以 ,解
,解 ,得
,得 ,
,
所以 的单调增区间为
的单调增区间为 . 4分
. 4分
(2)当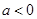 时,由
时,由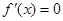 ,得
,得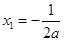 ,
,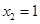 ,
,
①当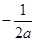 >1,即
>1,即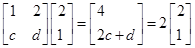 时,
时,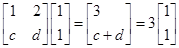 在
在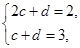 上是减函数,
上是减函数,
所以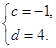 在
在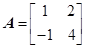 上的最小值为
上的最小值为 . 6分
. 6分
②当 ,即
,即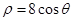 时,
时, 在
在

 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(1)设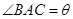 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为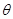 的函数
的函数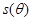 ;
;
(2)试确定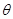 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.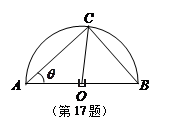
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的图象在点
的图象在点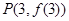 处的切线方程为
处的切线方程为 .
.
(1)求实数 的值;
的值;
(2)设 .
.
①若 是
是 上的增函数,求实数
上的增函数,求实数 的最大值;
的最大值;
②是否存在点 ,使得过点
,使得过点 的直线若能与曲线
的直线若能与曲线 围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点
围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com