Question

【题目】已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

（1）求的值；

（2）求的单调区间；

（3）设,其中为的导函数.证明：对任意.

Answer 1

【答案】（1）；（2）单调递增区间为；单调递减区间为；（3）详见解析.

【解析】

试题分析：（1）根据题意分析可能曲线在点处的切线与轴平行，等价于，从而；（2）由（1）可知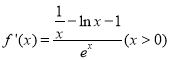，只需考虑分子的正负性即可，而，在上单调递减，再由，故当时，，，单调递增；当时，，，单调递减，∴单调递增区间为；单调递减区间为；（3），这是一指对相结合的函数，混在一起考虑其单调性比较复杂，因此考虑分开研究各自的取值情况：记，，，令，得，

当时，，单调递增；当时，，单调递减，

∴，即.

② 记，，，∴在上单调递减，

∴，即，综合①，②可知，.

试题解析：（1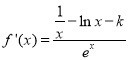），依题意，为所求；

（2）由（1）可知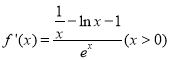，，记，，

∴在上单调递减，又∵，

∴当时，，，单调递增；当时，，，单调递减，∴单调递增区间为；单调递减区间为；

（3），

① 记，，，令，得，

当时，，单调递增；当时，，单调递减，

∴，即.

② 记，，，∴在上单调递减，

∴，即，综合①，②可知，.