【题目】已知
是数列
的前n项和，满足
，正项等比数列
的前n项和为
，且满足
.
(Ⅰ) 求数列{an}和{bn}的通项公式； (Ⅱ) 记
，求数列{cn}的前n项和
．
【答案】(Ⅰ) 
，
(Ⅱ) Gn＝n·2n＋1
【解析】
试题分析：（1）利用递推关系可得
．利用等比数列的通项公式及其前n项和公式可得
；（2）利用“错位相减法”与等比数列的前n项和公式即可得出
试题解析：(1) 
--------------------------3分
设等比数列{bn}的公比为q，首项为
，
依题意可知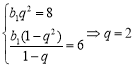
或
（舍）----5分
--------------------6分
(2) 则
2×2＋3×22＋4×23＋…＋n×2n－1 ＋(n＋1)×2n，
22×22＋3×23＋…＋(n－1)×2n－1＋n×2n＋(n＋1)2n＋1，……8分
所以－Gn＝2×2＋(22＋23＋…＋2n)－(n＋1)×2n＋1,
即－Gn＝2×2＋
－(n＋1)×2n＋1,--------------------10分
－Gn＝2×2＋
－(n＋1)×2n＋1
－Gn＝
－(n＋1)×2n＋1
－Gn＝－n×2n＋1
Gn＝n·2n＋1，n∈N*.----------------------------------------12分
科目：高中数学 来源： 题型：
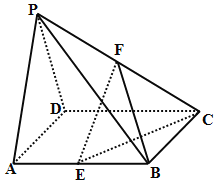
【题目】如图所示，在四棱锥P-ABCD中，底面ABCD是棱长为2的正方形，侧面PAD为正三角形，且面PAD⊥面ABCD，E、F分别为棱AB、PC的中点．
（1）求证：EF∥平面PAD；
（2）求三棱锥B-EFC的体积；
（3）求二面角P-EC-D的正切值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，有一段河流，河的一侧是以O为圆心，半径为
米的扇形区域OCD，河的另一侧是一段笔直的河岸l，岸边有一烟囱AB（不计B离河岸的距离），且OB的连线恰好与河岸l垂直，设OB与圆弧
的交点为E．经测量，扇形区域和河岸处于同一水平面，在点C，点O和点E处测得烟囱AB的仰角分别为
，
和
．
（1）求烟囱AB的高度；
（2）如果要在CE间修一条直路，求CE的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的导函数为
，
.
（1）当
时，求函数
的单调区间；
（2）若对满足
的一切
的值，都有
，求实数
的取值范围；
（3）若
对一切
恒成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系中，以坐标原点为极点，
轴为正半轴建立极坐标系，圆
的极坐标方程为
，直线
的参数方程为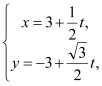
（t为参数）.
（1）求圆的直角坐标方程；
（2）求直线分圆所得的两弧程度之比.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如下图，已知四棱锥
中，底面
为菱形，
平面
，
，
，
分别是
，
的中点.
（I）证明：
平面
；
（II）取
，在线段
上是否存在点
，使得
与平面
所成最大角的正切值为
，若存在，请求出
点的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某飞机失联，经卫星侦查，其最后出现在小岛
附近，现派出四艘搜救船
，为方便联络，船
始终在以小岛为圆心，100海里为半径的圆上，船构成正方形编队展开搜索，小岛在正方形编队外（如图）.设小岛到
的距离为
，
，
船到小岛的距离为
.
（1）请分别求关于
的函数关系式
，并分别写出定义域；
（2）当两艘船之间的距离是多少时搜救范围最大（即最大）？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
