
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是棱
是棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
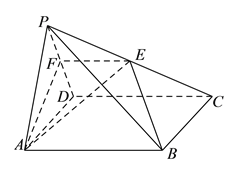
(![]() )求证:
)求证: ![]() .
.
(![]() )若
)若![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
求①二面角![]() 的锐二面角的余弦值.
的锐二面角的余弦值.
②在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
【答案】(1)证明见解析;(2)①![]() ;②答案见解析.
;②答案见解析.
【解析】试题分析:
(1)由题意可证得![]() 平面
平面![]() ,然后利用线面平行的性质定理可得
,然后利用线面平行的性质定理可得![]() ,
,
(2)①建立空间直角坐标系,由题意可得平面![]() 的一个法向量为
的一个法向量为![]() ;
;
而![]() 为平面
为平面![]() 的一个法向量.据此计算有二面角
的一个法向量.据此计算有二面角![]() 的锐二面角的余弦值为
的锐二面角的余弦值为![]() .
.
②假设![]() 上存在点
上存在点![]() 满足题意,利用平面向量的夹角公式得到关于实数
满足题意,利用平面向量的夹角公式得到关于实数![]() 的方程
的方程![]() ,解方程可得
,解方程可得![]() ,则线段
,则线段![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() .
.
试题解析:
(![]() )证明:∵
)证明:∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() ,
,
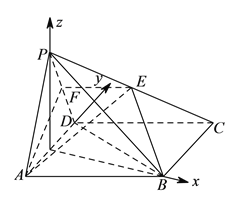
(![]() )①取
)①取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
,
∵![]() 是菱形,且
是菱形,且![]() ,
, ![]() ,
,
∴![]() ,
, ![]() 是等边三角形,
是等边三角形,
∴![]() ,
, ![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
以![]() 为原点,以
为原点,以![]() ,
, ![]() ,
, ![]() 为坐标轴建立空间坐标系
为坐标轴建立空间坐标系![]() ,则:
,则:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 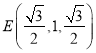 ,
, 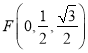 .
.
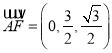 ,
, 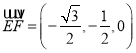 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
![]() ,∴
,∴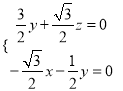 ,
,
令![]() 得:
得: ![]() ;
;
∵![]() 平面
平面![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
∴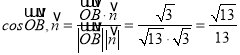 .
.
故二面角![]() 的锐二面角的余弦值为
的锐二面角的余弦值为![]() .
.
②假设![]() 上存在点
上存在点![]() 使得直线
使得直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() ,
,
则![]() 与
与![]() 所成夹角为
所成夹角为![]() ,
,
设![]() ,则:
,则:
![]() ,
,
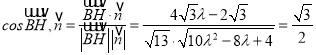 ,
,
化简得: ![]() ,
,
解得: ![]() 或
或![]() (舍),
(舍),
∴线段![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在(0, ![]() )内,sinx>cosx
)内,sinx>cosx
B.函数y=2sin(x+ ![]() )的图象的一条对称轴是x=
)的图象的一条对称轴是x= ![]() π
π
C.函数y= ![]() 的最大值为π
的最大值为π
D.函数y=sin2x的图象可以由函数y=sin(2x﹣ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据环境保护部《环境空气质量指数(![]() )技术规定》,空气质量指数(
)技术规定》,空气质量指数(![]() )在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
)在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
某城市空气质量监测部门对近300天空气中![]() 浓度进行统计,得出这300天
浓度进行统计,得出这300天![]() 浓度的频率分布直方图如图,将
浓度的频率分布直方图如图,将![]() 浓度落入各组的频率视为概率,并假设每天的
浓度落入各组的频率视为概率,并假设每天的![]() 浓度相互独立.
浓度相互独立.
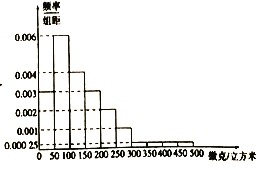
(1)求当地监测部门发布颜色预警的概率;
(2)据当地监测站数据显示未来4天将出现3天严重污染,求监测部门发布红色预警的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com